Dijagonalne matrice imaju najjednostavniju strukturu. Postavlja se pitanje da li je moguće pronaći osnovu u kojoj bi matrica linearnog operatora imala dijagonalni oblik. Takva osnova postoji.
Neka nam je dat linearni prostor R n i linearni operator A koji djeluje u njemu; u ovom slučaju, operator A uzima R n u sebe, to jest, A:R n → R n .
Definicija.
Vektor različit od nule naziva se sopstveni vektor operatora A ako se operator A prevodi u kolinearni vektor, tj. Broj λ se naziva svojstvena vrijednost ili svojstvena vrijednost operatora A, koja odgovara svojstvenom vektoru.
Napomenimo neka svojstva svojstvenih vrijednosti i sopstveni vektori.
1. Bilo koja linearna kombinacija vlastitih vektora 
operator A koji odgovara istoj svojstvenoj vrijednosti λ je svojstveni vektor sa istom svojstvenom vrijednošću.
2. Sopstveni vektori Operator A sa po parovima različitim sopstvenim vrednostima λ 1 , λ 2 , …, λ m su linearno nezavisni.
3. Ako su svojstvene vrijednosti λ 1 =λ 2 = λ m = λ, tada vlastita vrijednost λ odgovara ne više od m linearno nezavisnih svojstvenih vektora.
Dakle, ako postoji n linearno nezavisnih sopstvenih vektora 
, koje odgovaraju različitim svojstvenim vrijednostima λ 1, λ 2, ..., λ n, onda su linearno nezavisne, stoga se mogu uzeti kao osnova prostora R n. Nađimo oblik matrice linearnog operatora A u bazi njegovih vlastitih vektora, za koji ćemo djelovati s operatorom A na baznim vektorima: 
Onda 
.
Dakle, matrica linearnog operatora A u osnovi svojih svojstvenih vektora ima dijagonalni oblik, a svojstvene vrijednosti operatora A su duž dijagonale.
Postoji li još jedna osnova u kojoj matrica ima dijagonalni oblik? Odgovor na ovo pitanje daje sljedeća teorema.
Teorema. Matrica linearnog operatora A u bazi (i = 1..n) ima dijagonalni oblik ako i samo ako su svi vektori baze svojstveni vektori operatora A.
Pravilo za pronalaženje svojstvenih vrijednosti i svojstvenih vektora Neka je dat vektor
, gdje su x 1, x 2, …, x n koordinate vektora u odnosu na bazu 
i je svojstveni vektor linearnog operatora A koji odgovara svojstvenoj vrijednosti λ, tj. Ovaj odnos se može napisati u matričnom obliku 
. (*)
Jednačina (*) se može posmatrati kao jednačina za pronalaženje , i , odnosno, zanimaju nas netrivijalna rješenja, budući da svojstveni vektor ne može biti nula. Poznato je da su netrivijalna rješenja homogeni sistem linearne jednačine postoje ako i samo ako je det(A - λE) = 0. Dakle, da bi λ bila vlastita vrijednost operatora A neophodno je i dovoljno da je det(A - λE) = 0.
Ako je jednadžba (*) detaljno napisana u koordinatnom obliku, onda se dobija linearni sistem homogene jednačine:
(1)
Gdje 
- linearna operatorska matrica.
Sistem (1) nema br nulto rješenje, ako je njegova determinanta D jednaka nuli
Dobili smo jednačinu za pronalaženje vlastitih vrijednosti.
Ova jednačina se naziva karakteristična jednačina, a njena lijeva strana se naziva karakteristični polinom matrice (operator) A. Ako karakteristični polinom nema pravim korenima, tada matrica A nema svojstvene vektore i ne može se svesti na dijagonalni oblik.
Neka su λ 1, λ 2, …, λ n realni korijeni karakteristične jednadžbe, a među njima mogu biti višekratnici. Zamjenom ovih vrijednosti u sistem (1) nalazimo svojstvene vektore.
Primjer 12.
Linearni operator A djeluje u R 3 prema zakonu, gdje su x 1, x 2, .., x n koordinate vektora u bazi 
, 
, 
. Pronađite svojstvene vrijednosti i svojstvene vektore ovog operatora.
Rješenje.
Gradimo matricu ovog operatora: 
.
Kreiramo sistem za određivanje koordinata sopstvenih vektora: 
Sastavljamo karakterističnu jednačinu i rješavamo je: 
.
λ 1,2 = -1, λ 3 = 3.
Zamjenom λ = -1 u sistem imamo: 
ili 
Jer 
, tada postoje dvije zavisne varijable i jedna slobodna varijabla.
Neka je onda x 1 slobodna nepoznanica 
Ovaj sistem rješavamo na bilo koji način i nalazimo zajednička odluka ovog sistema: Osnovni sistem rješenja sastoji se od jednog rješenja, pošto je n - r = 3 - 2 = 1.
Skup svojstvenih vektora koji odgovaraju svojstvenoj vrijednosti λ = -1 ima oblik: , gdje je x 1 bilo koji broj osim nule. Odaberimo jedan vektor iz ovog skupa, na primjer, stavimo x 1 = 1: 
.
Slično razmišljajući, nalazimo svojstveni vektor koji odgovara svojstvenoj vrijednosti λ = 3: 
.
U prostoru R 3 baza se sastoji od tri linearno nezavisna vektora, ali smo dobili samo dva linearno nezavisna svojstvena vektora od kojih se ne može sastaviti baza u R 3. Prema tome, ne možemo svesti matricu A linearnog operatora na dijagonalni oblik.
Primjer 13.
Zadana matrica 
.
1. Dokazati da je vektor 
je svojstveni vektor matrice A. Nađite svojstvenu vrijednost koja odgovara ovom svojstvenom vektoru.
2. Naći bazu u kojoj matrica A ima dijagonalni oblik.
Rješenje.
1. Ako , Tada je svojstveni vektor 
.
Vektor (1, 8, -1) je svojstveni vektor. Svojstvena vrijednost λ = -1.
Matrica ima dijagonalni oblik u bazi koja se sastoji od svojstvenih vektora. Jedan od njih je poznat. Hajde da nađemo ostalo.
Tražimo sopstvene vektore iz sistema: 
Karakteristična jednačina: 
;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Nađimo svojstveni vektor koji odgovara svojstvenoj vrijednosti λ = -3: 
Rang matrice ovog sistema je dva i jednak broju nepoznanice, tako da ovaj sistem ima samo nulto rješenje x 1 = x 3 = 0. x 2 ovdje može biti bilo šta osim nule, na primjer, x 2 = 1. Dakle, vektor (0,1,0) je svojstveni vektor , što odgovara λ = -3. provjerimo: 
.
Ako je λ = 1, onda dobijamo sistem 
Rang matrice je dva. Precrtavamo posljednju jednačinu.
Neka je x 3 slobodna nepoznanica. Tada je x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Uz pretpostavku da je x 3 = 1, imamo (-3,-9,1) - svojstveni vektor koji odgovara svojstvenoj vrijednosti λ = 1. Provjerite: 
.
Budući da su vlastite vrijednosti realne i različite, vektori koji im odgovaraju su linearno nezavisni, pa se mogu uzeti kao osnova u R 3 . Dakle, u osnovi 
, 
, 
matrica A ima oblik: 
.
Ne može se svaka matrica linearnog operatora A:R n → R n svesti na dijagonalni oblik, jer za neke linearne operatore može postojati manje od n linearnih nezavisnih sopstvenih vektora. Međutim, ako je matrica simetrična, tada korijen karakteristične jednadžbe višestrukosti m odgovara točno m linearno neovisnih vektora.
Definicija.
Simetrična matrica je kvadratna matrica u kojoj su elementi simetrični oko glavne dijagonale jednaki, odnosno u kojoj su .
Bilješke.
1. Sve vlastite vrijednosti simetrične matrice su realne.
2. Svojstveni vektori simetrične matrice koji odgovaraju parno različitim svojstvenim vrijednostima su ortogonalni.
Kao jednu od brojnih primjena proučavanog aparata razmatramo problem određivanja tipa krive drugog reda.
Sa matricom A, ako postoji broj l takav da je AX = lX.
U ovom slučaju, broj l se naziva svojstvena vrijednost operatora (matrica A), koja odgovara vektoru X.
Drugim riječima, svojstveni vektor je vektor koji se pod djelovanjem linearnog operatora pretvara u kolinearni vektor, tj. samo pomnoži sa nekim brojem. Nasuprot tome, nepravilni vektori su složeniji za transformaciju.
Zapišimo definiciju sopstvenog vektora u obliku sistema jednačina:
Pomerimo sve pojmove na lijevu stranu:
Potonji sistem se može napisati u matričnom obliku na sljedeći način:
(A - lE)X = O
Rezultirajući sistem uvijek ima nulto rješenje X = O. Takvi sistemi u kojima su svi slobodni članovi jednaki nuli nazivaju se homogeni. Ako je matrica takvog sistema kvadratna i njena determinanta nije jednaka nuli, onda koristeći Cramerove formule uvijek dobijamo jedina odluka- nula. Može se dokazati da sistem ima različita od nule rješenja ako i samo ako je determinanta ove matrice jednaka nuli, tj.
|A - lE| = 
= 0
Ova jednačina sa nepoznatim l naziva se karakteristična jednačina (karakteristični polinom) matrice A (linearni operator).
Može se dokazati da karakteristični polinom linearnog operatora ne zavisi od izbora baze.
Na primjer, pronađimo svojstvene vrijednosti i svojstvene vektore linearnog operatora definirane matricom A =.
Da bismo to uradili, napravimo karakterističnu jednačinu |A - lE| = 
= (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; sopstvene vrijednosti l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12)/2 = 7.
Da bismo pronašli svojstvene vektore, rješavamo dva sistema jednačina
(A + 5E)X = O
(A - 7E)X = O
Za prvi od njih, proširena matrica poprima oblik
,
odakle je x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, tj. X (1) = (-(2/3)s; s).
Za drugu od njih, proširena matrica poprima oblik
,
odakle je x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, tj. X (2) = ((2/3)s 1; s 1).
Dakle, svojstveni vektori ovog linearnog operatora su svi vektori oblika (-(2/3)s; s) sa svojstvenom vrijednošću (-5) i svi vektori oblika ((2/3)s 1 ; s 1) sa svojstvena vrijednost 7 .
Može se dokazati da je matrica operatora A u bazi koju čine njegovi vlastiti vektori dijagonalna i ima oblik:
,
gdje su l i vlastite vrijednosti ove matrice.
Vrijedi i obrnuto: ako je matrica A u nekoj bazi dijagonalna, tada će svi vektori ove baze biti svojstveni vektori ove matrice.
Također se može dokazati da ako linearni operator ima n parno različitih svojstvenih vrijednosti, tada su odgovarajući svojstveni vektori linearno nezavisni, a matrica ovog operatora u odgovarajućoj bazi ima dijagonalni oblik.
Ilustrujmo ovo prethodnim primjerom. Uzmimo proizvoljne različite od nule vrijednosti c i c 1, ali takve da su vektori X (1) i X (2) linearno nezavisni, tj. predstavljalo bi osnovu. Na primjer, neka je c = c 1 = 3, zatim X (1) = (-2; 3), X (2) = (2; 3).
Hajde da se uverimo linearnu nezavisnost ovi vektori:
12 ≠ 0. U ovoj novoj bazi, matrica A će imati oblik A * = .
Da bismo to potvrdili, koristimo formulu A * = C -1 AC. Prvo, nađimo C -1.
C -1 = 
;
Kvadratni oblik f(x 1, x 2, x n) od n varijabli je zbir, čiji je svaki član ili kvadrat jedne od varijabli, ili proizvod dvije različite varijable, uzete sa određenim koeficijentom: f( x 1, x 2, x n ) = 
(a ij = a ji).
Matrica A sastavljena od ovih koeficijenata naziva se matrica kvadratnog oblika. Ovo je uvijek simetrična matrica (tj. matrica simetrična oko glavne dijagonale, a ij = a ji).
U matričnom zapisu, kvadratni oblik je f(X) = X T AX, gdje je
Zaista
Na primjer, zapišimo kvadratni oblik u matričnom obliku.
Da bismo to učinili, nalazimo matricu kvadratnog oblika. Njegovi dijagonalni elementi jednaki su koeficijentima varijabli na kvadrat, a preostali elementi jednaki su polovinama odgovarajućih koeficijenata kvadratnog oblika. Zbog toga
Neka se matrica-stupac varijabli X dobije nedegeneriranom linearnom transformacijom matrice-kolone Y, tj. X = CY, gdje je C nesingularna matrica n-tog reda. Tada je kvadratni oblik f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.
Dakle, s nedegeneriranom linearnom transformacijom C, matrica kvadratnog oblika ima oblik: A * = C T AC.
Na primjer, pronađimo kvadratni oblik f(y 1, y 2), dobijen iz kvadratnog oblika f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 linearnom transformacijom.
Kvadratni oblik se naziva kanonskim (ima kanonski oblik) ako su svi njegovi koeficijenti a ij = 0 za i ≠ j, tj.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .
Njegova matrica je dijagonalna.
Teorema (dokaz nije dat ovdje). Svaki kvadratni oblik se može svesti na kanonski oblik koristeći nedegenerisanu linearnu transformaciju.
Na primjer, smanjimo kvadratni oblik na kanonski oblik
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.
Da biste to učinili, prvo odaberite cijeli kvadrat s promjenljivom x 1:
f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.
Sada biramo ceo kvadrat sa promenljivom x 2:
f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.
Tada nedegenerirana linearna transformacija y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 i y 3 = x 3 dovodi ovaj kvadratni oblik u kanonski oblik f(y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .
Imajte na umu da je kanonski oblik kvadratnog oblika određen dvosmisleno (isti kvadratni oblik se može svesti na kanonski oblik Različiti putevi). Međutim, primljeno Različiti putevi kanonski oblici imaju niz opštih svojstava. Konkretno, broj članova s pozitivnim (negativnim) koeficijentima kvadratnog oblika ne ovisi o načinu svođenja forme na ovaj oblik (na primjer, u razmatranom primjeru uvijek će postojati dva negativna i jedan pozitivan koeficijent). Ovo svojstvo se zove zakon inercije kvadratnih oblika.
Provjerimo ovo dovođenjem istog kvadratnog oblika u kanonski oblik na drugačiji način. Započnimo transformaciju s varijablom x 2:
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, gdje je y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 i y 3 = x 1 . Evo negativan koeficijent-3 na y 1 i dva pozitivna koeficijenta 3 i 2 na y 2 i y 3 (a drugom metodom dobili smo negativan koeficijent (-5) na y 2 i dva pozitivna: 2 na y 1 i 1/20 na y 3 ).
Takođe treba napomenuti da je rang matrice kvadratnog oblika, koji se naziva rang kvadratnog oblika, jednak broju nenultih koeficijenata kanonskog oblika i da se ne menja pod linearnim transformacijama.
Kvadratni oblik f(X) naziva se pozitivno (negativno) određen ako je za sve vrijednosti varijabli koje nisu istovremeno jednake nuli pozitivan, tj. f(X) > 0 (negativno, tj.
f(X)< 0).
Na primjer, kvadratni oblik f 1 (X) = x 1 2 + x 2 2 je pozitivno određen, jer je zbir kvadrata, a kvadratni oblik f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 je negativno određen, jer predstavlja može se predstaviti kao f 2 (X) = -(x 1 - x 2) 2.
U većini praktičnih situacija je nešto teže utvrditi definitivni predznak kvadratnog oblika, pa za to koristimo jednu od sljedećih teorema (formulirat ćemo ih bez dokaza).
Teorema. Kvadratni oblik je pozitivno (negativno) određen ako i samo ako su sve vlastite vrijednosti njegove matrice pozitivne (negativne).
Teorema (Sylvesterov kriterij). Kvadratni oblik je pozitivno određen ako i samo ako su svi vodeći minori matrice ovog oblika pozitivni.
Glavni (ugaoni) minor k-tog reda matrice A n-tog reda je determinanta matrice, sastavljena od prvih k redova i stupaca matrice A ().
Imajte na umu da se za negativno određene kvadratne forme predznaci glavnih minora izmjenjuju, a minor prvog reda mora biti negativan.
Na primjer, hajde da ispitamo kvadratni oblik f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 radi definicije predznaka.
= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17; 
. Stoga je kvadratni oblik pozitivno određen.
Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 = 2 > 0. Glavni minor drugog reda D 2 = = 6 - 4 = 2 > 0. Prema tome, prema Sylvesterovom kriteriju, kvadratni oblik je pozitivno definitivno.
Ispitujemo još jedan kvadratni oblik za definitivnost znaka, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Metoda 1. Konstruirajmo matricu kvadratnog oblika A = . Karakteristična jednačina će imati oblik 
= (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17; 
. Stoga je kvadratni oblik negativno određen.
Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Prema tome, prema Sylvesterovom kriteriju, kvadratni oblik je negativno određen (znakovi glavnih minora se izmjenjuju, počevši od minusa).
I kao drugi primjer, ispitujemo znakom određen kvadratni oblik f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.
Metoda 1. Konstruirajmo matricu kvadratnog oblika A = . Karakteristična jednačina će imati oblik 
= (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41; 
.
Jedan od ovih brojeva je negativan, a drugi pozitivan. Znaci sopstvenih vrednosti su različiti. Prema tome, kvadratni oblik ne može biti ni negativno ni pozitivno određen, tj. ovaj kvadratni oblik nije znakom određen (može uzeti vrijednosti bilo kojeg predznaka).
Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 = 2 > 0. Glavni minor drugog reda D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
Kako umetnuti matematičke formule na web stranicu?
Ako ikada trebate dodati jednu ili dvije matematičke formule na web stranicu, onda je najlakši način da to učinite kao što je opisano u članku: matematičke formule se lako ubacuju na stranicu u obliku slika koje automatski generira Wolfram Alpha . Osim jednostavnosti, ova univerzalna metoda će pomoći u poboljšanju vidljivosti stranice tražilice. Radi već dugo (i mislim da će raditi zauvijek), ali je već moralno zastario.
Ako redovno koristite matematičke formule na svom sajtu, onda preporučujem da koristite MathJax - posebnu JavaScript biblioteku koja prikazuje matematičke zapise u web pretraživačima koristeći MathML, LaTeX ili ASCIIMathML markup.
Postoje dva načina da počnete koristiti MathJax: (1) pomoću jednostavnog koda možete brzo povezati MathJax skriptu na svoju web stranicu, koja će se automatski učitati sa udaljenog servera u pravo vrijeme (lista servera); (2) preuzmite MathJax skriptu sa udaljenog servera na vaš server i povežite ga sa svim stranicama vašeg sajta. Drugi metod - složeniji i dugotrajniji - ubrzaće učitavanje stranica vašeg sajta, a ako roditeljski MathJax server iz nekog razloga postane privremeno nedostupan, to ni na koji način neće uticati na vašu veb lokaciju. Unatoč ovim prednostima, odabrao sam prvi način jer je jednostavniji, brži i ne zahtijeva tehničke vještine. Slijedite moj primjer i za samo 5 minuta moći ćete koristiti sve mogućnosti MathJaxa na svojoj web stranici.
Možete povezati skriptu MathJax biblioteke sa udaljenog servera koristeći dvije opcije koda preuzete sa glavne MathJax web stranice ili na stranici dokumentacije:
Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kod vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake. Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako unesete prvi kod, morat ćete ga povremeno ažurirati. Ako umetnete drugi kod, stranice će se učitavati sporije, ali nećete morati stalno pratiti ažuriranja MathJaxa.
Najlakši način da povežete MathJax je u Blogger-u ili WordPress-u: u kontrolnu ploču web-mjesta dodajte widget dizajniran za umetanje JavaScript koda treće strane, kopirajte prvu ili drugu verziju koda za preuzimanje prikazanog iznad u njega i postavite widget bliže na početak šablona (usput, to uopće nije potrebno, pošto se MathJax skripta učitava asinhrono). To je sve. Sada naučite sintaksu označavanja MathML-a, LaTeX-a i ASCIIMathML-a i spremni ste da umetnete matematičke formule u web stranice svoje web stranice.
Svaki fraktal se konstruiše prema određenom pravilu, koje se dosledno primenjuje neograničen broj puta. Svako takvo vrijeme naziva se iteracija.
Iterativni algoritam za konstruisanje Mengerovog sunđera je prilično jednostavan: originalna kocka sa stranom 1 podeljena je ravninama paralelnim sa njenim plohama na 27 jednakih kocki. Iz nje se uklanja jedna središnja kocka i 6 susjednih kocki duž lica. Rezultat je set koji se sastoji od preostalih 20 manjih kockica. Učinivši isto sa svakom od ovih kockica, dobijamo set koji se sastoji od 400 manjih kockica. Nastavljajući ovaj proces beskonačno, dobijamo Menger sunđer.
www.site vam omogućava da pronađete. Stranica vrši proračun. Za nekoliko sekundi server će se oglasiti ispravno rješenje. Karakteristična jednačina za matricu će biti algebarski izraz , pronađen po pravilu za izračunavanje determinante matrice matrice, dok će duž glavne dijagonale postojati razlike u vrijednostima dijagonalnih elemenata i varijable. Prilikom izračunavanja karakteristične jednadžbe za matricu online, svaki element matrice će se pomnožiti s odgovarajućim drugim elementima matrice. Možete ga pronaći na mreži samo za kvadratnu matricu. Operacija pronalaženja karakteristične jednadžbe za online matricu svodi se na izračunavanje algebarskog zbroja umnoška elemenata matrice kao rezultat pronalaženja determinante matrice, samo u svrhu određivanja karakteristične jednadžbe za online matrica. Ova operacija zauzima posebno mjesto u teoriji matrica; omogućava vam da pronađete svojstvene vrijednosti i vektore koristeći korijene. Zadatak pronalaženja karakteristične jednadžbe za matricu na mreži sastoji se od množenja elemenata matrice i zatim sabiranja ovih proizvoda prema određenom pravilu. www.site pronalazi karakterističnu jednačinu za matricu date dimenzije na mreži. Izračunavanje karakteristične jednadžbe za matricu na mreži za datu dimenziju je pronalaženje polinoma sa numeričkim ili simboličkim koeficijentima, pronađenim prema pravilu za izračunavanje determinante matrice - kao zbir proizvoda odgovarajućih elemenata matrice, samo za svrhu određivanja karakteristične jednačine za matricu na mreži. Pronalaženje polinoma u odnosu na varijablu za kvadratnu matricu, kao definicija karakteristične jednadžbe za matricu, uobičajeno je u teoriji matrica. Vrijednost korijena polinoma karakteristične jednadžbe za online matricu se koristi za određivanje svojstvenih vektora i svojstvenih vrijednosti za matricu. Štoviše, ako je determinanta matrice jednaka nuli, tada će karakteristična jednadžba matrice i dalje postojati, za razliku od inverzne matrice. Da biste izračunali karakterističnu jednačinu za matricu ili pronašli karakteristične jednačine za više matrica odjednom, potrebno je uložiti mnogo vremena i truda, dok će naš server pronaći karakterističnu jednačinu za matricu online za nekoliko sekundi. U ovom slučaju, odgovor na pronalaženje karakteristične jednačine za online matricu će biti ispravan i sa dovoljnom preciznošću, čak i ako će brojevi prilikom pronalaženja karakteristične jednačine za online matricu biti iracionalni. Na web stranici www.site dozvoljeni su simbolični unosi u elemente matrice, odnosno karakteristična jednačina za online matricu može se prikazati u općenitom simboličkom obliku prilikom izračunavanja karakteristične jednačine online matrice. Korisno je provjeriti dobiveni odgovor prilikom rješavanja problema nalaženja karakteristične jednadžbe za matricu na mreži koristeći web stranicu www.site. Prilikom izvođenja operacije izračunavanja polinoma – karakteristične jednadžbe matrice, morate biti pažljivi i krajnje fokusirani prilikom rješavanja ovog problema. Zauzvrat, naša stranica će vam pomoći da provjerite svoje rješenje na temu karakteristične jednadžbe matrice na mreži. Ako nemate vremena za duge provjere riješenih problema, onda će www.site sigurno biti zgodan alat za provjeru prilikom pronalaženja i izračunavanja karakteristične jednadžbe za matricu na mreži.
"Prvi dio iznosi odredbe koje su minimalno potrebne za razumijevanje kemometrije, a drugi dio sadrži činjenice koje morate znati za dublje razumijevanje metoda multivarijantne analize. Prezentacija je ilustrovana primjerima napravljenim u Excel radnoj svesci Matrix.xls, koji prati ovaj dokument.
Veze na primjere se postavljaju u tekst kao Excel objekti. Ovi primjeri su apstraktne prirode i ni na koji način nisu vezani za probleme analitičke hemije. Pravi primjeri koristiti matrična algebra u kemometriji su obrađeni u drugim tekstovima koji pokrivaju različite kemometrijske primjene.
Većina mjerenja u analitičkoj hemiji nisu direktna, ali indirektno. To znači da se u eksperimentu, umjesto vrijednosti željenog analita C (koncentracija), dobije druga vrijednost x(signal), povezan, ali nije jednak C, tj. x(C) ≠ C. Po pravilu, vrsta zavisnosti x(C) nije poznato, ali na sreću u analitičkoj hemiji većina mjerenja je proporcionalna. To znači da sa povećanjem koncentracije C in a puta, signal X će se povećati za isti iznos, tj. x(a C) = sjekira(C). Osim toga, signali su i aditivni, pa će signal iz uzorka u kojem su prisutne dvije supstance sa koncentracijama C 1 i C 2 biti jednak zbiru signala svake komponente, tj. x(C 1 + C 2) = x(C 1)+ x(C 2). Proporcionalnost i aditivnost zajedno daju linearnost. Može se navesti mnogo primjera koji će ilustrirati princip linearnosti, ali dovoljno je spomenuti dva najveća sjajni primjeri- hromatografija i spektroskopija. Druga karakteristika svojstvena eksperimentu u analitičkoj hemiji je višekanalni. Moderna analitička oprema istovremeno mjeri signale za mnoge kanale. Na primjer, intenzitet propuštanja svjetlosti se mjeri za nekoliko talasnih dužina odjednom, tj. domet. Stoga se u eksperimentu bavimo mnogim signalima x 1 , x 2 ,...., x n, karakterišući skup koncentracija C 1 , C 2 , ..., C m supstanci prisutnih u sistemu koji se proučava.
Rice. 1 Spectra
Dakle, analitički eksperiment karakteriziraju linearnost i višedimenzionalnost. Stoga je zgodno eksperimentalne podatke posmatrati kao vektore i matrice i manipulirati njima pomoću aparata matrične algebre. Plodnost ovog pristupa ilustruje primer prikazan u, koji predstavlja tri spektra snimljena na 200 talasnih dužina od 4000 do 4796 cm −1. Prvi (x 1) i drugi (x 2) spektar dobijeni su za standardne uzorke u kojima su poznate koncentracije dvije supstance A i B: u prvom uzorku [A] = 0,5, [B] = 0,1 i u drugi uzorak [A] = 0,2, [B] = 0,6. Šta se može reći o novom, nepoznatom uzorku, čiji je spektar označen x 3?
Razmotrimo tri eksperimentalna spektra x 1, x 2 i x 3 kao tri vektora dimenzije 200. Koristeći linearnu algebru, lako možemo pokazati da je x 3 = 0,1 x 1 +0,3 x 2, dakle, u trećem uzorku samo supstance A i B su očigledno prisutni u koncentracijama [A] = 0,5×0,1 + 0,2×0,3 = 0,11 i [B] = 0,1×0,1 + 0,6×0,3 = 0,19.
1. Osnovne informacije 1.1 MatriceMatrix nazvana, na primjer, pravokutna tablica brojeva
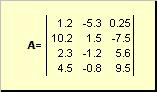
Rice. 2 Matrix
Matrice su označene velikim podebljanim slovima (A), a njihovi elementi odgovarajućim mala slova sa indeksima, tj. a ij. Prvi indeks numeriše redove, a drugi - kolone. U kemometriji je uobičajeno da se maksimalna vrijednost indeksa označava istim slovom kao i sam indeks, ali velikim slovima. Prema tome, matrica A se takođe može napisati kao ( a ij , i = 1,..., I; j = 1,..., J). Za primjer matrice I = 4, J= 3 i a 23 = −7.5.
Par brojeva I I J naziva se dimenzija matrice i označava se kao I× J. Primjer matrice u kemometriji je skup spektra dobivenih za I uzorci za J talasne dužine.
1.2. Najjednostavnije operacije sa matricamaMatrice mogu biti pomnožiti brojevima. U ovom slučaju, svaki element se množi ovim brojem. Na primjer -
Rice. 3 Množenje matrice brojem
Dvije matrice iste dimenzije mogu biti element po element fold I oduzimati. Na primjer,
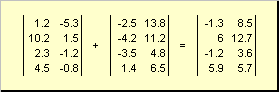
Rice. 4 Sabiranje matrice
Kao rezultat množenja brojem i sabiranja, dobiva se matrica iste dimenzije.
Nulta matrica je matrica koja se sastoji od nula. Označava se sa O. Očigledno, A +O = A, A −A = O i 0A = O.
Matrica može biti transponovati. Tokom ove operacije, matrica se okreće, tj. redovi i kolone se zamjenjuju. Transpozicija je označena prostim, A" ili indeksom A t. Dakle, ako je A = ( a ij , i = 1,..., I; j = 1,...,J), tada je A t = ( a ji , j = 1,...,J; i = 1,..., I). Na primjer
Rice. 5 Matrična transpozicija
Očigledno je da je (A t) t = A, (A + B) t = A t + B t.
1.3. Množenje matriceMatrice mogu biti umnožiti, ali samo ako imaju odgovarajuće dimenzije. Zašto je to tako, biće jasno iz definicije. Proizvod matrice A, dimenzija I× K, i matrica B, dimenzija K× J, nazvana matrica C, dimenzija I× J, čiji su elementi brojevi
Dakle, za proizvod AB potrebno je da broj stupaca u lijevoj matrici A bude jednak broju redova u desnoj matrici B. Primjer matričnog proizvoda -
Slika 6 Proizvod matrica
Pravilo za množenje matrice može se formulirati na sljedeći način. Da bi se pronašao element matrice C u raskrsnici i-ti red i j kolona ( c ij) mora se pomnožiti element po element i-ti red prve matrice A on j kolonu druge matrice B i zbrojiti sve rezultate. Dakle, u prikazanom primjeru, element iz trećeg reda i druge kolone dobija se kao zbir po elementima proizvoda trećeg reda A i drugog stupca B
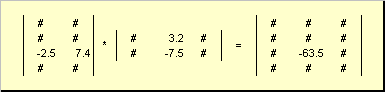
Slika 7 Element proizvoda matrica
Proizvod matrica zavisi od redosleda, tj. AB ≠ BA, barem iz dimenzionalnih razloga. Kažu da je nekomutativno. Međutim, proizvod matrica je asocijativan. To znači da je ABC = (AB)C = A(BC). Osim toga, ona je i distributivna, tj. A (B +C) = AB +AC. Očigledno AO = O.
1.4. Kvadratne matriceAko je broj stupaca matrice jednak broju njenih redova ( I = J=N), tada se takva matrica naziva kvadratna. U ovom dijelu ćemo razmotriti samo takve matrice. Među ovim matricama mogu se razlikovati matrice sa posebnim svojstvima.
Single matrica (označena I, a ponekad i E) je matrica u kojoj su svi elementi jednaki nuli, sa izuzetkom dijagonalnih, koji su jednaki 1, tj.
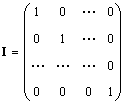
Očigledno AI = IA = A.
Matrica se zove dijagonala, ako su svi njegovi elementi osim dijagonalnih ( a ii) jednaki su nuli. Na primjer
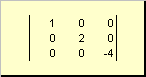
Rice. 8 Dijagonalna matrica
Matrica A se naziva gornja trouglasti, ako su svi njegovi elementi koji leže ispod dijagonale jednaki nuli, tj. a ij= 0, at i>j. Na primjer
Rice. 9 Gornja trokutasta matrica
Donja trokutasta matrica definirana je na sličan način.
Matrica A se zove simetrično, ako je A t = A . Drugim riječima a ij = a ji. Na primjer
Rice. 10 Simetrična matrica
Matrica A se zove ortogonalno, Ako
A t A = AA t = I .
Matrica se zove normalno Ako
1.5. Trag i determinantaSljedeći kvadratna matrica A (označena sa Tr(A) ili Sp(A)) je zbir njenih dijagonalnih elemenata,
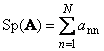
Na primjer,
Rice. 11 Trag matrice
Očigledno je da
Sp(α A ) = α Sp(A ) i
Sp(A +B) = Sp(A)+ Sp(B).
To se može pokazati
Sp(A) = Sp(A t), Sp(I) = N,
a takođe i to
Sp(AB) = Sp(BA).
Drugi važna karakteristika kvadratna matrica je njegova odrednica(označeno det(A )). Definicija determinante u opšti slučaj prilično komplikovano, pa ćemo početi s najjednostavnijom opcijom - matricom A dimenzije (2x2). Onda
Za (3×3) matricu determinanta će biti jednaka
U slučaju matrice ( N× N) determinanta se izračunava kao zbir 1·2·3· ... · N= N! pojmove, od kojih je svaki jednak
Indeksi k 1 , k 2 ,..., k N definirani su kao sve moguće uređene permutacije r brojevi u setu (1, 2, ..., N). Izračunavanje determinante matrice je složena procedura koja se u praksi provodi pomoću posebnih programa. Na primjer,
Rice. 12 Matrična determinanta
Napomenimo samo očigledna svojstva:
det(I ) = 1, det(A ) = det(A t),
det(AB) = det(A)det(B).
1.6. VektoriAko se matrica sastoji od samo jednog stupca ( J= 1), onda se takav objekat naziva vektor. Tačnije, vektor kolone. Na primjer
Također se mogu uzeti u obzir matrice koje se sastoje od jednog reda, na primjer
Ovaj objekt je također vektor, ali vektor reda. Prilikom analize podataka važno je razumjeti s kojim vektorima imamo posla – stupcima ili redovima. Dakle, spektar uzet za jedan uzorak može se smatrati vektorom reda. Tada skup spektralnih intenziteta na određenoj talasnoj dužini za sve uzorke treba tretirati kao vektor kolone.
Dimenzija vektora je broj njegovih elemenata.
Jasno je da se bilo koji vektor kolone može pretvoriti u vektor reda transpozicijom, tj.
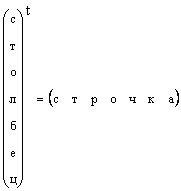
U slučajevima kada oblik vektora nije posebno specificiran, već se jednostavno kaže da je vektor, onda oni označavaju vektor stupca. I mi ćemo se pridržavati ovog pravila. Vektor je označen malim, uspravnim, podebljanim slovom. Nulti vektor je vektor čiji su svi elementi nula. Označen je kao 0.
1.7. Najjednostavnije operacije sa vektorimaVektori se mogu sabirati i množiti brojevima na isti način kao i matrice. Na primjer,
Rice. 13 Operacije s vektorima
Dva vektora x i y se nazivaju kolinearno, ako postoji broj α takav da
1.8. Proizvodi vektoraDva vektora iste dimenzije N može se umnožiti. Neka postoje dva vektora x = ( x 1 , x 2 ,...,x N) t i y = ( y 1 , y 2 ,...,y N) t . Vođeni pravilom množenja red po kolonu, od njih možemo sastaviti dva proizvoda: x t y i xy t. Prvi rad
pozvao skalar ili interni. Njegov rezultat je broj. Za to se također koristi oznaka (x ,y )= x t y. Na primjer,
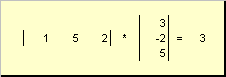
Rice. 14 Unutrašnji (skalarni) proizvod
Drugi komad
pozvao vanjski. Njegov rezultat je matrica dimenzija ( N× N). Na primjer,
Rice. 15 Eksterni rad
vektori, skalarni proizvod koji je jednak nuli nazivaju se ortogonalno.
1.9. Vektorska normaSkalarni proizvod vektora sa samim sobom naziva se skalarni kvadrat. Ova vrijednost
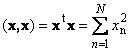
definira kvadrat dužina vektor x. Za označavanje dužine (takođe se naziva norma vektor) koristi se notacija
Na primjer,
Rice. 16 Vektorska norma
Vektor jedinične dužine (||x || = 1) naziva se normalizovan. Vektor različit od nule (x ≠ 0) može se normalizovati dijeljenjem sa njegovom dužinom, tj. x = ||x || (x/ ||x ||) = ||x || e. Ovdje je e = x/ ||x || - normalizovani vektor.
Vektori se nazivaju ortonormalni ako su svi normalizirani i po paru ortogonalni.
1.10. Ugao između vektoraSkalarni proizvod određuje i ugaoφ između dva vektora x i y
Ako su vektori ortogonalni, onda je cosφ = 0 i φ = π/2, a ako su kolinearni, onda je cosφ = 1 i φ = 0.
1.11. Vektorska reprezentacija matriceSvaka matrica A veličine I× J može se predstaviti kao skup vektora
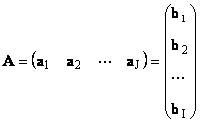
Ovdje svaki vektor a j je j kolonu i vektor reda b i je i red matrice A
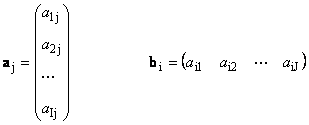
Vektori iste dimenzije ( N) može se dodati i pomnožiti brojem, baš kao matrice. Rezultat će biti vektor iste dimenzije. Neka postoji nekoliko vektora iste dimenzije x 1, x 2,...,x K i isti broj brojeva α α 1, α 2,...,α K. Vector
y = α 1 x 1 + α 2 x 2 +...+ α K x K
pozvao linearna kombinacija vektori x k .
Ako postoje takvi brojevi različiti od nule α k ≠ 0, k = 1,..., K da je y = 0, onda je takav skup vektora x k pozvao linearno zavisna. Inače se kaže da su vektori linearno nezavisni. Na primjer, vektori x 1 = (2, 2) t i x 2 = (−1, −1) t su linearno zavisni, jer x 1 +2x 2 = 0
1.13. Matrični rangRazmotrite skup K vektori x 1 , x 2 ,...,x K dimenzije N. Rang ovog sistema vektora je maksimalni broj linearno nezavisnih vektora. Na primjer u kompletu
postoje samo dva linearno nezavisna vektora, na primjer x 1 i x 2, pa je njegov rang 2.
Očigledno, ako postoji više vektora u skupu od njihove dimenzije ( K>N), onda su oni nužno linearno zavisni.
Matrični rang(označen sa rank(A)) je rang sistema vektora od kojih se sastoji. Iako se bilo koja matrica može predstaviti na dva načina (vektori stupca ili reda), to ne utiče na vrijednost ranga, jer
1.14. inverzna matricaKvadratna matrica A naziva se nesingularna ako ima jedinstvenu obrnuto matrica A -1 određena uslovima
AA −1 = A −1 A = I .
Inverzna matrica ne postoji za sve matrice. Neophodan i dovoljan uslov za nedegeneraciju je
det(A) ≠ 0 ili rang(A) = N.
Inverzija matrice je složena procedura za koju postoje posebni programi. Na primjer,
Rice. 17 Inverzija matrice
Predstavimo formule za najjednostavniji slučaj - matricu 2×2
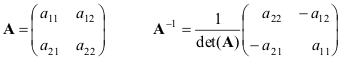
Ako su matrice A i B nesingularne, onda
(AB ) −1 = B −1 A −1 .
1.15. Pseudo inverzna matricaAko je matrica A singularna, a inverzna matrica ne postoji, tada u nekim slučajevima možete koristiti pseudoinverzno matrica, koja je definirana kao matrica A+ takva da
AA + A = A.
Pseudoinverzna matrica nije jedina i njen oblik zavisi od načina konstrukcije. Na primjer, za pravokutnu matricu možete koristiti Moore-Penroseov metod.
Ako je broj kolona manji broj linije, onda
A + =(A t A ) −1 A t
Na primjer,
Rice. 17a Pseudo-inverzija matrice
Ako je broj kolona više broja linije, onda
A + =A t (AA t) −1
1.16. Množenje vektora matricomVektor x se može pomnožiti sa matricom A odgovarajuće dimenzije. U ovom slučaju, vektor kolone se množi na desnoj Ax, a vektor reda se množi na lijevoj x t A. Ako je vektorska dimenzija J, i dimenziju matrice I× J tada će rezultat biti vektor dimenzija I. Na primjer,
Rice. 18 Množenje vektora matricom
Ako je matrica A kvadratna ( I× I), tada vektor y = Ax ima istu dimenziju kao x. Očigledno je da
A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .
Stoga se matrice mogu smatrati linearnim transformacijama vektora. Konkretno, Ix = x, Ox = 0.
2. Dodatne informacije 2.1. Sistemi linearnih jednačinaNeka je A matrica veličine I× J, a b je vektor dimenzija J. Razmotrite jednačinu
Ax = b
u odnosu na vektor x, dimenzija I. U suštini, to je sistem I linearne jednačine sa J nepoznato x 1 ,...,x J. Rješenje postoji ako i samo ako
rang(A) = rang(B) = R,
gdje je B matrica proširene dimenzije I×( J+1), koji se sastoji od matrice A dopunjene kolonom b, B = (A b). Inače, jednačine su nekonzistentne.
Ako R = I = J, onda je rješenje jedinstveno
x = A −1 b .
Ako R < I, tada postoji mnogo različitih rješenja koja se mogu izraziti kroz linearnu kombinaciju J−R vektori. Sistem homogenih jednadžbi Ax = 0 sa kvadratnom matricom A ( N× N) ima netrivijalno rješenje (x ≠ 0) ako i samo ako je det(A) = 0. Ako je R= rang(A) 0.
Slično definisano negativan(x t Ax< 0), nenegativan(x t Ax ≥ 0) i negativan(x t Ax ≤ 0) određene matrice.
2.4. Cholesky decompositionAko je simetrična matrica A pozitivno određena, tada postoji jedinstvena trokutasta matrica U sa pozitivnim elementima za koje
A = U t U .
Na primjer,
Rice. 19 Cholesky dekompozicija
2.5. Polarna dekompozicijaNeka je A nesingularna kvadratna matrica dimenzija N× N. Zatim postoji jedinstvena polar performanse
A = SR,
gdje je S nenegativna simetrična matrica, a R je ortogonalna matrica. Matrice S i R se mogu eksplicitno definirati:
S 2 = AA t ili S = (AA t) ½ i R = S −1 A = (AA t) −½ A .
Na primjer,
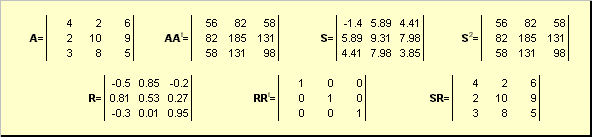
Rice. 20 Polarna dekompozicija
Ako je matrica A singularna, onda dekompozicija nije jedinstvena – naime: S je i dalje jedan, ali može biti mnogo R. Polarna dekompozicija predstavlja matricu A kao kombinaciju kompresije/proširenja S i rotacije R.
2.6. Sopstveni vektori i sopstvene vrednostiNeka je A kvadratna matrica. Vektor v se zove svojstveni vektor matrica A ako
Av = λv,
gdje se zove broj λ eigenvalue matrice A. Dakle, transformacija koju matrica A izvodi na vektoru v se svodi na jednostavno rastezanje ili kompresiju sa koeficijentom λ. Svojstveni vektor je određen do množenja konstantom α ≠ 0, tj. ako je v svojstveni vektor, onda je i αv svojstveni vektor.
2.7. Svojstvene vrijednostiMatrica A ima dimenziju ( N× N) ne može biti više od N sopstvene vrijednosti. Oni zadovoljavaju karakteristična jednačina
det(A − λI ) = 0,
biće algebarska jednačina N-th red. Konkretno, za matricu 2×2 karakteristična jednačina ima oblik
Na primjer,
Rice. 21 Sopstvene vrijednosti
Skup svojstvenih vrijednosti λ 1 ,..., λ N matrica A se zove spektra A.
Spektar ima različita svojstva. Posebno
det(A ) = λ 1 ×...×λ N, Sp(A ) = λ 1 +...+λ N.
Svojstvene vrijednosti proizvoljne matrice mogu biti kompleksni brojevi, ali ako je matrica simetrična (A t = A), tada su njene svojstvene vrijednosti realne.
2.8. Vlastiti vektoriMatrica A ima dimenziju ( N× N) ne može biti više od N sopstveni vektori, od kojih svaki odgovara svom eigenvalue. Da bi se odredio svojstveni vektor v n potrebno je riješiti sistem homogenih jednačina
(A − λ n I ) v n = 0 .
Ima netrivijalno rješenje, budući da det(A − λ n I ) = 0.
Na primjer,
Rice. 22 Sopstveni vektori
Svojstveni vektori simetrične matrice su ortogonalni.