Fourierovi nizovi periodičnih funkcija s periodom 2π.
Fourierov red nam omogućava da proučavamo periodične funkcije razlažući ih na komponente. Tipične su naizmjenične struje i naponi, pomaci, brzina i ubrzanje koljenastog mehanizma i zvučni valovi praktični primjeri primjena periodičnih funkcija u inženjerskim proračunima.
Proširenje Fourierovog reda zasniva se na pretpostavci da svi imaju praktični značaj funkcije u intervalu -π ≤x≤ π mogu se izraziti u obliku konvergentnih trigonometrijskih nizova (serija se smatra konvergentnom ako se niz parcijalnih suma sastavljen od njegovih članova konvergira):
Standardna (=obična) notacija kroz zbir sinx i cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
gdje su a o, a 1,a 2,...,b 1,b 2,.. realne konstante, tj.
Gdje se, za raspon od -π do π, koeficijenti Fourierovog reda izračunavaju pomoću formula:

Koeficijenti a o , a n i b n nazivaju se Fourierovi koeficijenti, a ako se mogu pronaći, onda se serija (1) naziva blizu Fouriera, što odgovara funkciji f(x). Za seriju (1), pojam (a 1 cosx+b 1 sinx) naziva se prvi ili osnovni harmonik,
Drugi način za pisanje niza je korištenje relacije acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Gdje je a o konstanta, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 su amplitude različitih komponenti i jednako je a n =arctg a n /b n.
Za niz (1), termin (a 1 cosx+b 1 sinx) ili c 1 sin(x+α 1) naziva se prvi ili osnovni harmonik, (a 2 cos2x+b 2 sin2x) ili c 2 sin(2x +α 2) naziva se drugi harmonik i tako dalje.
Za precizno predstavljanje složenog signala obično je potreban beskonačan broj pojmova. Međutim, u mnogim praktičnim problemima dovoljno je razmotriti samo prvih nekoliko pojmova.
Fourierovi nizovi neperiodičnih funkcija s periodom 2π.
Proširenje neperiodičnih funkcija.
Ako je funkcija f(x) neperiodična, to znači da se ne može proširiti u Fourierov red za sve vrijednosti x. Međutim, moguće je definirati Fourierov red koji predstavlja funkciju u bilo kojem rasponu širine 2π.
S obzirom na neperiodičnu funkciju, nova funkcija se može konstruirati odabirom vrijednosti f(x) unutar određenog raspona i ponavljanjem izvan tog raspona u intervalima od 2π. Budući da je nova funkcija periodična s periodom 2π, može se proširiti u Fourierov red za sve vrijednosti x. Na primjer, funkcija f(x)=x nije periodična. Međutim, ako ga je potrebno proširiti u Fourierov niz u intervalu od o do 2π, onda se izvan ovog intervala konstruira periodična funkcija s periodom od 2π (kao što je prikazano na donjoj slici).

Za neperiodične funkcije kao što je f(x)=x, zbir Fourierovog reda je jednak vrijednosti f(x) u svim tačkama u datom rasponu, ali nije jednak f(x) za tačke izvan dometa. Da bi se pronašao Fourierov red neperiodične funkcije u rasponu 2π, koristi se ista formula Fourierovih koeficijenata.
Parne i neparne funkcije.
Kažu da je funkcija y=f(x) parna ako je f(-x)=f(x) za sve vrijednosti x. Grafovi parnih funkcija su uvijek simetrični u odnosu na y-os (to jest, oni su zrcalne slike). Dva primjera parnih funkcija: y=x2 i y=cosx.
Za funkciju y=f(x) se kaže da je neparna ako je f(-x)=-f(x) za sve vrijednosti x. Grafovi neparnih funkcija su uvijek simetrični u odnosu na ishodište.
Mnoge funkcije nisu ni parne ni neparne.
Proširenje Fourierovog reda u kosinusima.
Fourierov red parne periodične funkcije f(x) s periodom 2π sadrži samo kosinusne članove (tj. nema sinusne članove) i može uključivati konstantan član. dakle,

gdje su koeficijenti Furijeovog reda,

Fourierov red neparne periodične funkcije f(x) sa periodom 2π sadrži samo članove sa sinusima (tj. ne sadrži članove sa kosinusima).
dakle,

gdje su koeficijenti Furijeovog reda,
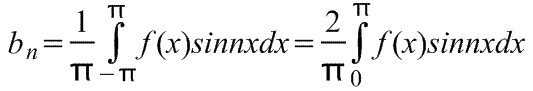
Fourierov niz u poluciklusu.
Ako je funkcija definirana za raspon, recimo od 0 do π, a ne samo od 0 do 2π, može se proširiti u niz samo u sinusima ili samo u kosinusima. Rezultirajući Fourierov red naziva se Fourierov red poluciklusa.
Ako želite dobiti poluciklusnu Fourierovu ekspanziju kosinusa funkcije f(x) u rasponu od 0 do π, tada morate konstruirati parnu periodičnu funkciju. Na sl. Ispod je funkcija f(x)=x, izgrađena na intervalu od x=0 do x=π. Zbog ravnomjerna funkcija simetrično oko f(x) ose, nacrtajte liniju AB, kao što je prikazano na sl. ispod. Ako pretpostavimo da je izvan razmatranog intervala rezultujući trokutasti oblik periodičan sa periodom od 2π, onda konačni graf izgleda ovako: na sl. ispod. Budući da moramo dobiti Fourierovu ekspanziju u kosinusima, kao i prije, izračunavamo Fourierove koeficijente a o i a n

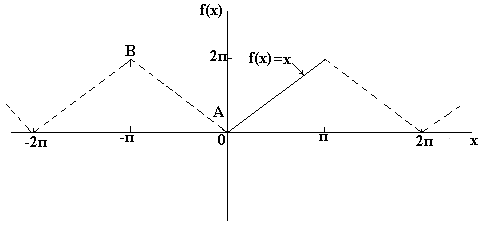
Ako želite dobiti Fourierovu ekspanziju poluciklusa u smislu sinusa funkcije f(x) u rasponu od 0 do π, tada morate konstruirati neparnu periodičnu funkciju. Na sl. Ispod je funkcija f(x)=x, izgrađena na intervalu od x=0 do x=π. Zbog neparna funkcija simetrično u odnosu na ishodište, konstruišemo liniju CD, kao što je prikazano na sl. Ako pretpostavimo da je izvan razmatranog intervala rezultujući pilasti signal periodičan sa periodom od 2π, tada konačni graf ima oblik prikazan na Sl. Budući da moramo dobiti Fourierovu ekspanziju poluciklusa u smislu sinusa, kao i prije, izračunavamo Fourierov koeficijent. b

Fourierov red za proizvoljan interval.
Proširenje periodične funkcije s periodom L.
Periodična funkcija f(x) se ponavlja kako se x povećava za L, tj. f(x+L)=f(x). Prijelaz sa prethodno razmatranih funkcija s periodom od 2π na funkcije s periodom od L je prilično jednostavan, jer se može izvršiti promjenom varijable.
Da bismo pronašli Fourierov red funkcije f(x) u opsegu -L/2≤x≤L/2, uvodimo novu varijablu u tako da funkcija f(x) ima period od 2π u odnosu na u. Ako je u=2πx/L, tada je x=-L/2 za u=-π i x=L/2 za u=π. Također neka je f(x)=f(Lu/2π)=F(u). Fourierov red F(u) ima oblik
(Granice integracije mogu se zamijeniti bilo kojim intervalom dužine L, na primjer, od 0 do L)
Fourierov red na poluperiodu za funkcije specificirane u intervalu L≠2π.
Za supstituciju u=πh/L, interval od x=0 do x=L odgovara intervalu od u=0 do u=π. Posljedično, funkcija se može proširiti u niz samo u kosinusima ili samo u sinusima, tj. u Fourierov niz u poluperiodu.
Kosinusna ekspanzija u rasponu od 0 do L ima oblik

Fourierovi nizovi periodičnih funkcija s periodom 2π.
Fourierov red nam omogućava da proučavamo periodične funkcije razlažući ih na komponente. Naizmjenične struje i naponi, pomaci, brzina i ubrzanje koljenastih mehanizama i akustični valovi tipični su praktični primjeri korištenja periodičnih funkcija u inženjerskim proračunima.
Proširenje Fourierovog reda temelji se na pretpostavci da se sve funkcije od praktične važnosti u intervalu -π ≤x≤ π mogu izraziti u obliku konvergentnih trigonometrijskih redova (niz se smatra konvergentnim ako je niz parcijalnih suma sastavljen od njegovih članova konvergira):
Standardna (=obična) notacija kroz zbir sinx i cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
gdje su a o, a 1,a 2,...,b 1,b 2,.. realne konstante, tj.
Gdje se, za raspon od -π do π, koeficijenti Fourierovog reda izračunavaju pomoću formula:

Koeficijenti a o , a n i b n nazivaju se Fourierovi koeficijenti, a ako se mogu naći, onda se niz (1) naziva Fourierov red koji odgovara funkciji f (x). Za seriju (1), pojam (a 1 cosx+b 1 sinx) naziva se prvi ili osnovni harmonik,
Drugi način za pisanje niza je korištenje relacije acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Gdje je a o konstanta, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 su amplitude različitih komponenti i jednako je a n =arctg a n /b n.
Za niz (1), termin (a 1 cosx+b 1 sinx) ili c 1 sin(x+α 1) naziva se prvi ili osnovni harmonik, (a 2 cos2x+b 2 sin2x) ili c 2 sin(2x +α 2) naziva se drugi harmonik i tako dalje.
Za precizno predstavljanje složenog signala obično je potreban beskonačan broj pojmova. Međutim, u mnogim praktičnim problemima dovoljno je razmotriti samo prvih nekoliko pojmova.
Fourierovi nizovi neperiodičnih funkcija s periodom 2π.
Proširenje neperiodičnih funkcija.
Ako je funkcija f(x) neperiodična, to znači da se ne može proširiti u Fourierov red za sve vrijednosti x. Međutim, moguće je definirati Fourierov red koji predstavlja funkciju u bilo kojem rasponu širine 2π.
S obzirom na neperiodičnu funkciju, nova funkcija se može konstruirati odabirom vrijednosti f(x) unutar određenog raspona i ponavljanjem izvan tog raspona u intervalima od 2π. Budući da je nova funkcija periodična s periodom 2π, može se proširiti u Fourierov red za sve vrijednosti x. Na primjer, funkcija f(x)=x nije periodična. Međutim, ako ga je potrebno proširiti u Fourierov niz u intervalu od o do 2π, onda se izvan ovog intervala konstruira periodična funkcija s periodom od 2π (kao što je prikazano na donjoj slici).

Za neperiodične funkcije kao što je f(x)=x, zbir Fourierovog reda je jednak vrijednosti f(x) u svim tačkama u datom rasponu, ali nije jednak f(x) za tačke izvan dometa. Da bi se pronašao Fourierov red neperiodične funkcije u rasponu 2π, koristi se ista formula Fourierovih koeficijenata.
Parne i neparne funkcije.
Kažu da je funkcija y=f(x) parna ako je f(-x)=f(x) za sve vrijednosti x. Grafovi parnih funkcija su uvijek simetrični u odnosu na y-os (to jest, oni su zrcalne slike). Dva primjera parnih funkcija: y=x2 i y=cosx.
Za funkciju y=f(x) se kaže da je neparna ako je f(-x)=-f(x) za sve vrijednosti x. Grafovi neparnih funkcija su uvijek simetrični u odnosu na ishodište.
Mnoge funkcije nisu ni parne ni neparne.
Proširenje Fourierovog reda u kosinusima.
Fourierov red parne periodične funkcije f(x) s periodom 2π sadrži samo kosinusne članove (tj. nema sinusne članove) i može uključivati konstantan član. dakle,

gdje su koeficijenti Furijeovog reda,

Fourierov red neparne periodične funkcije f(x) sa periodom 2π sadrži samo članove sa sinusima (tj. ne sadrži članove sa kosinusima).
dakle,

gdje su koeficijenti Furijeovog reda,
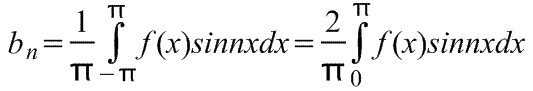
Fourierov niz u poluciklusu.
Ako je funkcija definirana za raspon, recimo od 0 do π, a ne samo od 0 do 2π, može se proširiti u niz samo u sinusima ili samo u kosinusima. Rezultirajući Fourierov red naziva se Fourierov red poluciklusa.
Ako želite dobiti poluciklusnu Fourierovu ekspanziju kosinusa funkcije f(x) u rasponu od 0 do π, tada morate konstruirati parnu periodičnu funkciju. Na sl. Ispod je funkcija f(x)=x, izgrađena na intervalu od x=0 do x=π. Pošto je parna funkcija simetrična u odnosu na f(x) os, povlačimo liniju AB, kao što je prikazano na sl. ispod. Ako pretpostavimo da je izvan razmatranog intervala rezultujući trokutasti oblik periodičan sa periodom od 2π, onda konačni graf izgleda ovako: na sl. ispod. Budući da moramo dobiti Fourierovu ekspanziju u kosinusima, kao i prije, izračunavamo Fourierove koeficijente a o i a n

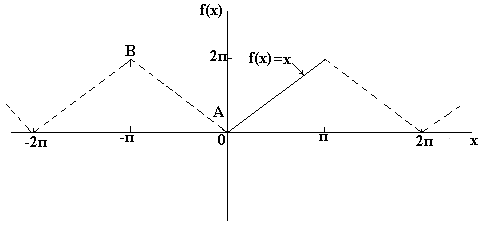
Ako želite dobiti Fourierovu ekspanziju poluciklusa u smislu sinusa funkcije f(x) u rasponu od 0 do π, tada morate konstruirati neparnu periodičnu funkciju. Na sl. Ispod je funkcija f(x)=x, izgrađena na intervalu od x=0 do x=π. Pošto je neparna funkcija simetrična u odnosu na ishodište, konstruišemo liniju CD, kao što je prikazano na Sl. Ako pretpostavimo da je izvan razmatranog intervala rezultujući pilasti signal periodičan sa periodom od 2π, tada konačni graf ima oblik prikazan na Sl. Budući da moramo dobiti Fourierovu ekspanziju poluciklusa u smislu sinusa, kao i prije, izračunavamo Fourierov koeficijent. b

Fourierov red za proizvoljan interval.
Proširenje periodične funkcije s periodom L.
Periodična funkcija f(x) se ponavlja kako se x povećava za L, tj. f(x+L)=f(x). Prijelaz sa prethodno razmatranih funkcija s periodom od 2π na funkcije s periodom od L je prilično jednostavan, jer se može izvršiti promjenom varijable.
Da bismo pronašli Fourierov red funkcije f(x) u opsegu -L/2≤x≤L/2, uvodimo novu varijablu u tako da funkcija f(x) ima period od 2π u odnosu na u. Ako je u=2πx/L, tada je x=-L/2 za u=-π i x=L/2 za u=π. Također neka je f(x)=f(Lu/2π)=F(u). Fourierov red F(u) ima oblik
(Granice integracije mogu se zamijeniti bilo kojim intervalom dužine L, na primjer, od 0 do L)
Fourierov red na poluperiodu za funkcije specificirane u intervalu L≠2π.
Za supstituciju u=πh/L, interval od x=0 do x=L odgovara intervalu od u=0 do u=π. Posljedično, funkcija se može proširiti u niz samo u kosinusima ili samo u sinusima, tj. u Fourierov niz u poluperiodu.
Kosinusna ekspanzija u rasponu od 0 do L ima oblik

Mnogi procesi koji se dešavaju u prirodi i tehnologiji imaju tendenciju da se ponavljaju u određenim intervalima. Takvi procesi se nazivaju periodični i matematički se opisuju periodičnim funkcijama. Takve funkcije uključuju grijeh(x) , cos(x) , grijeh(wx), cos(wx) . Zbir dvije periodične funkcije, na primjer, funkcija oblika , generalno govoreći, više nije periodično. Ali može se dokazati da ako je odnos w 1 / w 2 je racionalan broj, onda je ovaj zbir periodična funkcija.
Najjednostavniji periodični procesi - harmonijske oscilacije - opisuju se periodičnim funkcijama grijeh(wx) I cos(wx). Složeniji periodični procesi opisuju se funkcijama koje se sastoje od konačnog ili beskonačnog broja članova oblika grijeh(wx) I cos(wx).
3.2. Trigonometrijski niz. Fourierovi koeficijentiRazmotrimo funkcionalnu seriju oblika:
Ova serija se zove trigonometrijski; brojevi A 0 , b 0 , a 1 , b 1 ,A 2 , b 2 …, a n , b n ,… su pozvani koeficijenti trigonometrijske serije. Serija (1) se često piše na sljedeći način:
 .
(2)
.
(2)
Pošto članovi trigonometrijskog niza (2) imaju zajednički period  , tada je suma niza, ako konvergira, također periodična funkcija s periodom
, tada je suma niza, ako konvergira, također periodična funkcija s periodom  .
.
Pretpostavimo da je funkcija f(x) je zbir ove serije:
 .
(3)
.
(3)
U ovom slučaju kažu da je funkcija f(x)
proširen je u trigonometrijski niz. Uz pretpostavku da ovaj niz konvergira ravnomjerno na intervalu  , možete odrediti njegove koeficijente koristeći formule:
, možete odrediti njegove koeficijente koristeći formule:
 ,
,  ,
, .
(4)
.
(4)
Zovu se koeficijenti niza koji su određeni ovim formulama Fourierovi koeficijenti.
Trigonometrijski redovi (2), čiji su koeficijenti određeni Fourierovim formulama (4), nazivaju se blizu Fouriera, što odgovara funkciji f(x).
Dakle, ako je periodična funkcija f(x) je zbir konvergentnog trigonometrijskog reda, onda je ovaj niz njegov Fourierov red.
3.3. Konvergencija Fourierovih redovaFormule (4) pokazuju da se Fourierovi koeficijenti mogu izračunati za bilo koju integrabilnu vrijednost na intervalu 
 -periodična funkcija, tj. Za takvu funkciju uvijek možete konstruirati Fourierov niz. Ali hoće li se ovaj niz konvergirati funkciji f(x)
i pod kojim uslovima?
-periodična funkcija, tj. Za takvu funkciju uvijek možete konstruirati Fourierov niz. Ali hoće li se ovaj niz konvergirati funkciji f(x)
i pod kojim uslovima?
Podsjetimo da je funkcija f(x), definisano na segmentu [ a; b] , naziva se komadično glatkim ako on i njegov derivat nemaju više od konačnog broja diskontinuiteta prve vrste.
Sljedeća teorema daje dovoljne uslove dekompozibilnost funkcije u Fourierovom redu.
Dirichletova teorema. Neka  -periodična funkcija f(x)
je glatko na komade
-periodična funkcija f(x)
je glatko na komade  . Tada njegov Fourierov red konvergira na f(x)
na svakoj od njegovih tačaka kontinuiteta i na vrijednost 0,5(f(x+0)+
f(x-0))
na prelomnoj tački.
. Tada njegov Fourierov red konvergira na f(x)
na svakoj od njegovih tačaka kontinuiteta i na vrijednost 0,5(f(x+0)+
f(x-0))
na prelomnoj tački.
Primjer 1.
Proširite funkciju u Fourierov niz f(x)=
x, specificirano na intervalu  .
.
Rješenje. Ova funkcija zadovoljava Dirichletove uslove i stoga se može proširiti u Fourierov red. Koristeći formule (4) i metodu integracije po dijelovima  , nađimo Furijeove koeficijente:
, nađimo Furijeove koeficijente:


Dakle, Fourierov red za funkciju f(x) ima pogled.
Kako umetnuti matematičke formule na web stranicu?
Ako ikada trebate dodati jednu ili dvije matematičke formule na web stranicu, najlakši način da to učinite je kako je opisano u članku: matematičke formule se lako ubacuju na web stranicu u obliku slika koje automatski generira Wolfram Alpha . Osim jednostavnosti, ova univerzalna metoda pomoći će poboljšanju vidljivosti stranice tražilice. Radi već dugo (i mislim da će raditi zauvijek), ali je već moralno zastario.
Ako redovno koristite matematičke formule na svom sajtu, onda preporučujem da koristite MathJax - posebnu JavaScript biblioteku koja prikazuje matematičke zapise u web pretraživačima koristeći MathML, LaTeX ili ASCIIMathML markup.
Postoje dva načina da počnete koristiti MathJax: (1) pomoću jednostavnog koda možete brzo povezati MathJax skriptu na svoju web stranicu, koja će se automatski učitati sa udaljenog servera u pravo vrijeme (lista servera); (2) preuzmite MathJax skriptu sa udaljenog servera na vaš server i povežite ga sa svim stranicama vašeg sajta. Drugi metod - složeniji i dugotrajniji - ubrzaće učitavanje stranica vaše stranice, a ako roditeljski MathJax server iz nekog razloga postane privremeno nedostupan, to ni na koji način neće utjecati na vašu vlastitu stranicu. Unatoč ovim prednostima, odabrao sam prvi metod jer je jednostavniji, brži i ne zahtijeva tehničke vještine. Slijedite moj primjer i za samo 5 minuta moći ćete koristiti sve mogućnosti MathJaxa na svojoj web stranici.
Možete povezati skriptu biblioteke MathJax sa udaljenog servera koristeći dvije opcije koda preuzete sa glavne MathJax web stranice ili na stranici dokumentacije:
Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kod vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake. Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako unesete prvi kod, morat ćete ga povremeno ažurirati. Ako umetnete drugi kod, stranice će se učitavati sporije, ali nećete morati stalno pratiti ažuriranja MathJaxa.
Najlakši način za povezivanje MathJax-a je u Blogger-u ili WordPress-u: u kontrolnu ploču web-mjesta dodajte widget dizajniran za umetanje JavaScript koda treće strane, kopirajte prvu ili drugu verziju koda za preuzimanje prikazanog iznad u njega i postavite widget bliže na početak šablona (usput, to uopće nije potrebno, pošto se MathJax skripta učitava asinhrono). To je sve. Sada naučite sintaksu označavanja MathML-a, LaTeX-a i ASCIIMathML-a i spremni ste da umetnete matematičke formule u web stranice svoje web stranice.
Svaki fraktal se konstruiše prema određenom pravilu, koje se dosledno primenjuje neograničen broj puta. Svako takvo vrijeme naziva se iteracija.
Iterativni algoritam za konstruisanje Mengerovog sunđera je prilično jednostavan: originalna kocka sa stranom 1 podeljena je ravninama paralelnim sa njenim plohama na 27 jednakih kocki. Iz nje se uklanja jedna središnja kocka i 6 susjednih kocki duž lica. Rezultat je set koji se sastoji od preostalih 20 manjih kockica. Učinivši isto sa svakom od ovih kockica, dobijamo set koji se sastoji od 400 manjih kockica. Nastavljajući ovaj proces beskonačno, dobijamo Menger sunđer.
Transkript1 MINISTARSTVO OBRAZOVANJA I NAUKE RF DRŽAVNI UNIVERZITET NOVOSIBIRSK FIZIČKI FAKULTET R. K. Belkheeva FOURIER SERIES U PRIMJERIMA I PROBLEMIMA Udžbenik Novosibirsk 211
2 UDC BBK V161 B44 B44 Belkheeva R.K. Fourierov niz u primjerima i zadacima: Udžbenik / Novosibirsk. stanje univ. Novosibirsk, s. ISBN B udžbenik Date su osnovne informacije o Fourierovim redovima, dati su primjeri za svaku proučavanu temu. Detaljno je analiziran primjer primjene Fourierove metode za rješavanje problema poprečnih vibracija strune. Dostavljen je ilustrativni materijal. Postoje zadaci za samostalno rješavanje. Namijenjeno studentima i nastavnicima Fizičkog fakulteta NSU. Objavljeno odlukom metodološke komisije Fizičkog fakulteta NSU. Recenzent: Dr. Phys.-Math. Sci. V. A. Aleksandrov Priručnik je pripremljen kao deo implementacije Programa razvoja NRU-NSU za godine. ISBN iz Novosibirska Državni univerzitet, 211 c Belkheeva R.K., 211
3 1. Proširivanje 2π-periodične funkcije u Fourierov red Definicija. Fourierov red funkcije f(x) je funkcionalni red a 2 + (a n cosnx + b n sin nx), (1) gdje se koeficijenti a n, b n izračunavaju pomoću formula: a n = 1 π b n = 1 π f (x) cosnxdx, n = , 1,..., (2) f(x) sin nxdx, n = 1, 2,.... (3) Formule (2) (3) se zovu Eulerove Fourierove formule. Činjenica da funkcija f(x) odgovara Fourierovom redu (1) zapisuje se kao formula f(x) a 2 + (a n cosnx + b n sin nx) (4) i kaže se da desni deo formula (4) je formalni Fourierov niz funkcije f(x). Drugim riječima, formula (4) znači samo da su koeficijenti a n, b n pronađeni pomoću formula (2), (3). 3
4 Definicija. 2π-periodična funkcija f(x) naziva se komadično glatkom ako postoji konačan broj točaka = x u intervalu [, π]< x 1 . Рассмотрим два условия: а) f(l x) = f(x); б) f(l + x) = f(x), x [, l/2]. С geometrijska tačka U smislu gledišta, uslov (a) znači da je graf funkcije f(x) simetričan u odnosu na vertikalnu liniju x = l/2, a uslov (b) da je graf funkcije f(x) centralno simetričan u odnosu na tačku (l/2;) na osi apscise. Onda pošteno sljedeće izjave: 1) ako je funkcija f(x) parna i uslov (a) je zadovoljen, tada je b 1 = b 2 = b 3 =... =, a 1 = a 3 = a 5 =... = ; 2) ako je funkcija f(x) parna i uslov (b) je zadovoljen, tada je b 1 = b 2 = b 3 =... =, a = a 2 = a 4 =... = ; 3) ako je funkcija f(x) neparna i uslov (a) je zadovoljen, tada je a = a 1 = a 2 =... =, b 2 = b 4 = b 6 =... = ; 4) ako je funkcija f(x) neparna i uslov (b) je zadovoljen, tada je a = a 1 = a 2 =... =, b 1 = b 3 = b 5 =... =. ZADACI U zadacima 1 7 nacrtajte grafove i pronađite Fourierove redove za funkcije (pod pretpostavkom da imaju period od 2π: ako< x a cosx + a2 В задачах найдите ряды Фурье в комплексной форме для функций. 26. f(x) = sgn x, π < x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46
47 5. Ljapunovljev teorem jednakosti (Ljapunovljeva jednakost). Neka je funkcija f: [, π] R takva da je f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47
48 a n = 2 π f(x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. Prema tome, Ljapunovljeva jednakost za funkciju f(x) ima oblik: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. Iz posljednje jednakosti za a π nalazimo sin 2 na n 2 = a(π a) 2 Postavljanjem a = π 2, dobijamo sin2 na = 1 za n = 2k 1 i sin 2 na = za n = 2k. Prema tome, k=1 1 (2k 1) 2 = = π2 8. PRIMJER 14. Zapišimo Ljapunovljevu jednakost za funkciju f(x) = x cosx, x [, π] i koristimo je da pronađemo zbir broja serija (4n 2 + 1) 2 (4n 2 1) 4. 1 π Rješenje. Direktni proračuni daju = π π f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π 1 4π cos 2xdx =
49 Pošto je f(x) parna funkcija, onda za sve n imamo b n =, a n = 2 π = 1 π 1 = π(n + 1) = f(x) cosnxdx = 2 π 1 cos(n + 1 )x π (n + 1) 2 x cosxcosnxdx = x (cos(n + 1)x + cos(n 1)x) dx = 1 π sin(n + 1)xdx sin(n 1)xdx = π(n 1) π π 1 + cos(n 1)x = π(n 1) 2 1 (= (1) (n+1) 1) 1 (+ (1) (n+1) 1) = π(n + 1) 2 π(n 1) 2 () = (1)(n+1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1)(n+1) 1 n k π (n 2 1) = π (4k 2 1) 2, ako je n = 2k, 2, ako je n = 2k + 1. Koeficijent a 1 se mora posebno izračunati, jer u opšta formula kod n = 1 imenilac razlomka postaje nula. = 1 π a 1 = 2 π f(x) cosxdx = 2 π x(1 + cos 2x)dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.
50 Dakle, Ljapunovljeva jednakost za funkciju f(x) ima oblik: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π, odakle nalazimo zbir niza brojeva (4n 2 + 1) 2 (4n 2 1) = π π ZADACI 32. Napišite Ljapunovljevu jednakost za funkciju ( x f(x) = 2 πx, ako je x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по racionalne funkcije: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Izvedite složeni oblik generalizovane Ljapunovljeve jednakosti. 36. Pokazati da složeni oblik Ljapunovljeve jednakosti vrijedi ne samo za funkcije realne vrijednosti, već i za funkcije kompleksne vrijednosti. 5
51 π (2n + 1) = π sin 2απ 2απ = 2sin2 απ α 2 π 2 Odgovori + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f(x)g(x) dx= c n d n, gdje je c n Furijeov koeficijent 2π funkcije f(x), a d n je funkcija Fourierovog koeficijenta g(x). 6. Diferencijacija Fourierovih redova Neka je f: R R kontinuirano diferencibilna 2π-periodična funkcija. Njegov Fourierov red ima oblik: f(x) = a 2 + (a n cos nx + b n sin nx). Izvod f (x) ove funkcije bit će kontinuirana i 2π-periodična funkcija, za koju možemo napisati formalni Fourierov red: f (x) a 2 + (a n cos nx + b n sin nx), gdje je a, a n , b n, n = 1 , 2,... Fourierovi koeficijenti funkcije f (x). 51
52 Teorema (o diferencijaciji Fourierovih redova po članu). Pod gornjim pretpostavkama, jednakosti a =, a n = nb n, b n = na n, n 1 vrijede. PRIMJER 15. Neka je glatka funkcija f(x) kontinuirana u intervalu [, π]. Dokažimo da ako je zadovoljen uvjet f(x)dx =, vrijedi nejednakost 2 dx 2 dx, nazvana Steklova nejednakost, i pobrinućemo se da jednakost u njoj vrijedi samo za funkcije oblika f(x) = A cosx. Drugim riječima, Steklova nejednakost daje uslove pod kojima malenost derivacije (u srednjem kvadratu) implicira malenost funkcije (u srednjem kvadratu). Rješenje. Proširimo funkciju f(x) na interval [, ] na paran način. Označimo proširenu funkciju istim simbolom f(x). Tada će proširena funkcija biti kontinuirana i glatka po komadima na intervalu [, π]. Kako je funkcija f(x) kontinuirana, onda je f 2 (x) kontinuirana na intervalu i 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52
53 Pošto je kontinuirana funkcija parna, onda je b n =, a = po uvjetu. Prema tome, Ljapunovljeva jednakost ima oblik 1 π 2 dx = a 2 π n. (17) Uvjerimo se da je za f (x) zadovoljen zaključak teoreme o diferencijaciji Fourierovog reda po članu, odnosno da je a =, a n = nb n, b n = na n, n 1. Neka derivacija f (x) ima kinkove u tačkama x 1, x 2,..., x N u intervalu [, π]. Označimo x =, x N+1 = π. Podijelimo interval integracije [, π] na N +1 intervala (x, x 1),..., (x N, x N+1), na svakom od kojih je f(x) kontinuirano diferencibilan. Zatim, koristeći svojstvo aditivnosti integrala, a zatim integrirajući po dijelovima, dobijamo: b n = 1 π = 1 π = 1 π f (x) sin nxdx = 1 π N f(x) sin nx j= N f (x) sin nx j= x j+1 x j x j+1 x j n n π N j= x j+1 x j x j+1 x j f (x) sin nxdx = f(x) cosnxdx = f(x) cosnxdx = = 1 π [(f(x 1) sin nx 1 f(x) sin nx) + + (f(x 2) sinnx 2 f(x 1) sin nx 1)
54 + (f(x N+1) sin nx N+1 f(x N) sin nx N)] na n = = 1 π na n = = 1 π na n = na n. x j+1 a = 1 f (x)dx = 1 N f (x)dx = π π j= x j = 1 N x j+1 f(x) π = 1 (f(π) f()) = . x j π j= Posljednja jednakost se javlja zbog činjenice da je funkcija f(x) nastavljena na paran način, što znači f(π) = f(). Slično dobijamo a n = nb n. Pokazali smo da je teorema o diferencijaciji Fourierovih redova po članu za kontinuiranu komadno glatku 2π-periodičnu funkciju čiji izvod u intervalu [, π] podliježe diskontinuitetima prve vrste ispravan. To znači f (x) a 2 + (a n cosnx + b n sin nx) = (na n)sin nx, pošto je a =, a n = nb n =, b n = na n, n = 1, 2,.... Od 2 dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)
55 Pošto je svaki član u nizu u (18) veći ili jednak odgovarajućem članu u nizu u (17), onda je 2 dx 2 dx. Podsjećajući da je f(x) paran nastavak originalne funkcije, imamo 2 dx 2 dx. Što dokazuje Steklova jednakost. Sada ćemo ispitati za koje funkcije važi jednakost u Steklovoj nejednakosti. Ako je za barem jedan n 2 koeficijent a n različit od nule, tada je a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55
56 PROBLEMI 37. Neka je glatka funkcija f(x) kontinuirana u intervalu [, π]. Dokažite da kada je uslov f() = f(π) = zadovoljen, nejednakost 2 dx 2 dx, koja se naziva i Steklova nejednakost, vrijedi i uvjerite se da jednakost u njoj vrijedi samo za funkcije oblika f(x) = B sin x. 38. Neka je funkcija f neprekidna u intervalu [, π] i ima u sebi (osim možda konačnog broja tačaka) izvod f (x) koji je kvadratno integrabilan. Dokažite da ako su ispunjeni uslovi f() = f(π) i f(x) dx =, onda nejednakost 2 dx 2 dx, nazvana Wirtingerova nejednakost, vrijedi i jednakost u njoj vrijedi samo za funkcije oblika f (x ) = A cosx + B sin x. 56
57 7. Primjena Fourierovih redova za rješavanje parcijalnih diferencijalnih jednadžbi Prilikom proučavanja realnog objekta (prirodne pojave, proizvodni proces, sistemi upravljanja itd.) dva faktora se pokazuju značajnim: nivo akumuliranog znanja o predmetu koji se proučava i stepen razvijenosti matematičkog aparata. On moderna pozornica naučno istraživanje Razvijen je sljedeći lanac: fenomen fizički model matematički model. Fizička formulacija (model) problema je sljedeća: identificiraju se uslovi za razvoj procesa i glavni faktori koji na njega utiču. Matematička formulacija (model) se sastoji od opisa faktora i uslova odabranih u fizičkoj formulaciji u obliku sistema jednačina (algebarskih, diferencijalnih, integralnih, itd.). Problem se naziva dobro postavljenim ako u određenom funkcionalnom prostoru postoji rješenje problema, jedinstveno i kontinuirano ovisi o početnim i graničnim uvjetima. Matematički model nije identičan predmetu koji se razmatra, ali je njegov približan opis. Izvođenje jednadžbe za slobodne male poprečne vibracije strune. Neka krajevi uzice budu učvršćeni, a sama struna zategnuta. Ako pomaknete tetivu iz njenog ravnotežnog položaja (na primjer, povučete je nazad ili udarite), tada će struna početi na 57
58 oklijevaj. Pretpostavićemo da se sve tačke strune kreću okomito na njen ravnotežni položaj (poprečne vibracije), a u svakom trenutku struna leži u istoj ravni. Uzmimo sistem pravougaonih koordinata xou u ovoj ravni. Tada, ako je u početnom trenutku vremena t = struna bila locirana duž ose Ox, tada će u značiti odstupanje strune od ravnotežnog položaja, odnosno položaj tačke strune sa apscisom x na proizvoljan trenutak vremena t odgovara vrijednosti funkcije u(x, t). Za svaku fiksnu vrijednost t, graf funkcije u(x, t) predstavlja oblik vibrirajuće žice u trenutku t (slika 32). Pri konstantnoj vrijednosti x, funkcija u(x, t) daje zakon gibanja tačke sa apscisom x duž prave linije paralelne s Ou osi, izvod u t je brzina ovog kretanja, a drugi izvod je 2 u t 2 ubrzanje. Rice. 32. Sile primijenjene na infinitezimalni dio niza Napravimo jednačinu koju funkcija u(x, t) mora zadovoljiti. Da bismo to učinili, napravit ćemo još nekoliko pojednostavljenih pretpostavki. Smatraćemo da je niz apsolutno fleksibilan - 58
59 koy, odnosno pretpostavit ćemo da struna nije otporna na savijanje; to znači da su naponi koji nastaju u struni uvijek usmjereni tangencijalno na njen trenutni profil. Pretpostavlja se da je struna elastična i podložna Hookeovom zakonu; to znači da je promjena veličine sile zatezanja proporcionalna promjeni dužine strune. Pretpostavimo da je niz homogen; to znači da je njegova linearna gustina ρ konstantna. Zanemarujemo vanjske sile. To znači da razmatramo slobodne vibracije. Proučavaćemo samo male vibracije strune. Ako sa ϕ(x, t) označimo ugao između ose apscise i tangente na niz u tački sa apscisom x u trenutku t, tada je uslov za male oscilacije da je vrijednost ϕ 2 (x, t) se može zanemariti u poređenju sa ϕ (x, t), odnosno ϕ 2. Pošto je ugao ϕ mali, onda se cosϕ 1, ϕ sin ϕ tan ϕ u, dakle, može zanemariti i vrednost (u x x,) 2. Odmah slijedi da tokom procesa vibracija možemo zanemariti promjenu dužine bilo kojeg dijela strune. Zaista, dužina komada žice M 1 M 2, projektovanog u interval ose apscise, gde je x 2 = x 1 + x, jednaka je l = x 2 x () 2 u dx x. x Pokažimo da će, pod našim pretpostavkama, veličina sile zatezanja T biti konstantna duž cijele strune. Za ovo, uzmimo bilo koji dio niza M 1 M 2 (slika 32) u trenutku t i zamijenimo djelovanje odbačenih dijelova - 59
60 silama zatezanja T 1 i T 2. Kako se, prema uslovu, sve tačke strune kreću paralelno sa Ou osom i nema spoljnih sila, zbir projekcija sila zatezanja na osu Ox mora biti jednak nuli: T 1 cosϕ(x 1, t) + T 2 cosϕ(x 2, t) =. Dakle, zbog malenosti uglova ϕ 1 = ϕ(x 1, t) i ϕ 2 = ϕ(x 2, t), zaključujemo da je T 1 = T 2. Označimo opšte značenje T 1 = T 2 do T. Sada izračunajmo zbir projekcija F u istih sila na osu Ou: F u = T sin ϕ(x 2, t) T sin ϕ(x 1, t). (2) Kako za male uglove sin ϕ(x, t) tan ϕ(x, t), i tan ϕ(x, t) u(x, t)/ x, onda se jednačina (2) može prepisati kao F u T (tg ϕ(x 2, t) tan ϕ(x 1, t)) (u T x (x 2, t) u) x (x 1, t) x x T 2 u x 2(x 1, t) x . Pošto je tačka x 1 izabrana proizvoljno, onda je F u T 2 u x2(x, t) x. Nakon što su pronađene sve sile koje djeluju na presjek M 1 M 2, na njega primjenjujemo drugi Newtonov zakon, prema kojem je proizvod mase i ubrzanja jednak zbroju svih aktivne snage. Masa komada uzice M 1 M 2 jednaka je m = ρ l ρ x, a ubrzanje je jednako 2 u(x, t). Newtonova t 2 jednadžba ima oblik: 2 u t (x, t) x = u 2 α2 2 x2(x, t) x, gdje je α 2 = T ρ konstantan pozitivan broj. 6
61 Smanjenjem za x, dobijamo 2 u t (x, t) = u 2 α2 2 x2(x, t). (21) Kao rezultat, dobili smo linearnu homogenu parcijalnu diferencijalnu jednačinu drugog reda sa konstantni koeficijenti. Zove se jednadžba vibracija strune ili jednodimenzionalna valna jednačina. Jednačina (21) je u suštini preformulacija Newtonovog zakona i opisuje kretanje strune. Ali u fizičkoj formulaciji problema postojali su zahtjevi da krajevi žice budu fiksirani i da je pozicija žice u nekom trenutku poznata. Ove uslove ćemo zapisati kao jednačine na sledeći način: a) pretpostavićemo da su krajevi niza fiksirani u tačkama x = i x = l, tj. pretpostavićemo da su za sve t relacije u(, t) =, u (l, t ) = ; (22) b) pretpostavićemo da se u trenutku t = pozicija niza poklapa sa grafikom funkcije f(x), tj. pretpostavićemo da je za sve x [, l] jednakost u(x,) = f( x); (23) c) pretpostavićemo da je u trenutku t = tačka niza sa apscisom x data brzina g(x), odnosno pretpostavićemo da je u (x,) = g(x). (24) t Relacije (22) nazivaju se granični uslovi, a relacije (23) i (24) se nazivaju početni uslovi. Matematički model slobodnih malih transverzala 61
62 oscilacije strune je da je potrebno riješiti jednadžbu (21) sa graničnim uvjetima (22) i početnim uvjetima (23) i (24) Rješavanje jednačine slobodnih malih poprečnih oscilacija strune Furijeovom metodom Rješavanje jednačine (21) u regija x l,< t . Подставляя (25) в (21), получим: X T = α 2 X T, (26) или T (t) α 2 T(t) = X (x) X(x). (27) Говорят, что произошло разделение переменных. Так как x и t не зависят друг от друга, то левая часть в (27) не зависит от x, а правая от t и общая величина этих отношений 62
63 mora biti konstanta, koju označavamo sa λ: T (t) α 2 T(t) = X (x) X(x) = λ. Odavde dobijamo dva obična diferencijalne jednadžbe: X (x) λx(x) =, (28) T (t) α 2 λt(t) =. (29) U ovom slučaju, granični uslovi (22) će imati oblik X()T(t) = i X(l)T(t) =. Pošto oni moraju biti zadovoljeni za sve t, t >, onda je X() = X(l) =. (3) Nađimo rješenja jednačine (28) koja zadovoljavaju granične uslove (3). Razmotrimo tri slučaja. Slučaj 1: λ >. Označimo λ = β 2. Jednačina (28) ima oblik X (x) β 2 X(x) =. Njegovo karakteristična jednačina k 2 β 2 = ima korijen k = ±β. dakle, zajednička odluka jednačina (28) ima oblik X(x) = C e βx + De βx. Moramo odabrati konstante C i D tako da su ispunjeni granični uslovi (3), tj. X() = C + D =, X(l) = C e βl + De βl =. Pošto je β, onda ovaj sistem jednačina ima jedina odluka C=D=. Dakle, X(x) i 63
64 u(x, t). Tako smo u slučaju 1 dobili trivijalno rješenje koje nećemo dalje razmatrati. Slučaj 2: λ =. Tada jednačina (28) poprima oblik X (x) = i njeno rješenje je očigledno dato formulom: X(x) = C x+d. Zamjenom ovog rješenja u granične uslove (3) dobijamo X() = D = i X(l) = Cl =, što znači C = D =. Dakle, X(x) i u(x, t), i opet imamo trivijalno rješenje. Slučaj 3: λ
