Tangenta je prava linija , koji dodiruje graf funkcije u jednoj tački i čije su sve tačke na najkraćoj udaljenosti od grafa funkcije. Prema tome, tangenta prelazi tangentu na graf funkcije pod određeni ugao a nekoliko tangenti pod različitim uglovima ne može proći kroz tačku dodira. Tangentne jednadžbe i normalne jednadžbe na graf funkcije konstruiraju se pomoću izvoda.

Jednačina tangente je izvedena iz jednačine linije .

Izvedemo jednadžbu tangente, a zatim i jednadžbu normale na graf funkcije.

y = kx + b .

U njemu k- ugaoni koeficijent.

Odavde dobijamo sledeći unos:

y - y 0 = k(x - x 0 ) .

Vrijednost derivata f "(x 0 ) funkcije y = f(x) u tački x0 jednak nagibu k= tg φ tangenta na graf funkcije povučen kroz tačku M0 (x 0 , y 0 ) , Gdje y0 = f(x 0 ) . Ovo je geometrijsko značenje derivacije .

Dakle, možemo zamijeniti k on f "(x 0 ) i dobijete sljedeće jednadžba tangente na graf funkcije :

y - y 0 = f "(x 0 )(x - x 0 ) .

U problemima koji uključuju sastavljanje jednadžbe tangente na graf funkcije (a uskoro ćemo prijeći na njih), potrebno je jednadžbu dobivenu iz gornje formule svesti na jednačina prave linije u opštem obliku. Da biste to učinili, trebate premjestiti sva slova i brojeve na lijevu stranu jednačine, a ostaviti nulu na desnoj strani.

Sada o normalnoj jednadžbi. Normalno - ovo je prava linija koja prolazi kroz tačku tangente na graf funkcije okomita na tangentu. Normalna jednačina :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

Da biste se zagrijali, od vas se traži da sami riješite prvi primjer, a zatim pogledate rješenje. S razlogom se nadamo da ovaj zadatak neće biti „hladan tuš“ za naše čitatelje.

Primjer 0. Kreirajte jednadžbu tangente i normalnu jednačinu za graf funkcije u tački M (1, 1) .

Primjer 1. Napišite jednadžbu tangente i normalnu jednačinu za graf funkcije , ako je apscisa tangenta .

Nađimo derivaciju funkcije:

Sada imamo sve što treba zamijeniti u unosu datom u teorijskoj pomoći da se dobije jednačina tangente. Dobijamo

U ovom primjeru imali smo sreće: ispostavilo se da je nagib nula, tako da nije bilo potrebe da se jednadžba posebno svodi na njen opći oblik. Sada možemo kreirati normalnu jednačinu:

Na slici ispod: graf funkcije u bordo boji, tangenta Zelena boja, narandžasta normalna.

Sljedeći primjer također nije kompliciran: funkcija je, kao i u prethodnom, također polinom, ali nagib neće biti jednak nuli, pa će se dodati još jedan korak - dovođenje jednačine u opći oblik.

Primjer 2.

Rješenje. Nađimo ordinatu tangentne tačke:

Nađimo derivaciju funkcije:

Nađimo vrijednost derivacije u tački tangente, odnosno nagib tangente:

Sve dobijene podatke zamenimo u „praznu formulu“ i dobijemo tangentnu jednačinu:

Dovodimo jednadžbu u njen opći oblik (sakupljamo sva slova i brojeve osim nule na lijevoj strani, a ostavljamo nulu na desnoj):

Sastavljamo normalnu jednačinu:

Primjer 3. Napišite jednadžbu tangente i jednadžbu normale na graf funkcije ako je apscisa tačka tangente.

Rješenje. Nađimo ordinatu tangentne tačke:

Nađimo derivaciju funkcije:

Nađimo vrijednost derivacije u tački tangente, odnosno nagib tangente:

Pronalazimo tangentnu jednačinu:

Prije nego što dovedete jednadžbu u njen opći oblik, trebate je malo "pročešljati": pomnožite član po član sa 4. Ovo radimo i dovedemo jednačinu u njen opći oblik:

Sastavljamo normalnu jednačinu:

Primjer 4. Napišite jednadžbu tangente i jednadžbu normale na graf funkcije ako je apscisa tačka tangente.

Rješenje. Nađimo ordinatu tangentne tačke:

Nađimo derivaciju funkcije:

Nađimo vrijednost derivacije u tački tangente, odnosno nagib tangente:

Dobijamo tangentnu jednačinu:

Dovodimo jednačinu u njen opći oblik:

Sastavljamo normalnu jednačinu:

Uobičajena greška pri pisanju tangentnih i normalnih jednačina je da se ne primijeti da je funkcija data u primjeru složena i da se njen izvod izračuna kao izvod jednostavne funkcije. Sljedeći primjeri su već iz složene funkcije(odgovarajuća lekcija će se otvoriti u novom prozoru).

Primjer 5. Napišite jednadžbu tangente i jednadžbu normale na graf funkcije ako je apscisa tačka tangente.

Rješenje. Nađimo ordinatu tangentne tačke:

Pažnja! Ova funkcija- kompleksno, budući da argument tangente (2 x) je sama po sebi funkcija. Stoga derivaciju funkcije nalazimo kao derivaciju kompleksne funkcije.

On moderna pozornica razvoj obrazovanja, jedan od njegovih glavnih zadataka je formiranje kreativno misleće ličnosti. Sposobnost za kreativnost kod učenika se može razviti samo ako su sistematski uključeni u osnove istraživačke aktivnosti. Osnova da učenici koriste svoje kreativne moći, sposobnosti i talente su formirana punopravna znanja i vještine. S tim u vezi, problem formiranja sistema osnovnih znanja i vještina za svaku temu školski kurs matematika je od velike važnosti. U isto vrijeme, moraju biti punopravne vještine didaktičke svrhe ne pojedinačni zadaci, već pažljivo osmišljen sistem istih. U najširem smislu, sistem se shvata kao skup međusobno povezanih elemenata koji imaju integritet i stabilnu strukturu.

Razmotrimo tehniku za podučavanje učenika kako da napišu jednačinu za tangentu na graf funkcije. U suštini, svi problemi nalaženja tangentne jednačine svode se na potrebu da se iz skupa (snopa, familije) linija izaberu one koje zadovoljavaju određeni zahtjev – one su tangente na graf određene funkcije. U ovom slučaju, skup linija iz kojih se vrši odabir može se specificirati na dva načina:

a) tačka koja leži na ravni xOy (centralna olovka pravih);
b) ugaoni koeficijent (paralelni snop pravih linija).

S tim u vezi, prilikom proučavanja teme „Tangenta na graf funkcije“ kako bismo izolovali elemente sistema, identifikovali smo dve vrste problema:

1) zadaci na tangentu zadanu tačkom kroz koju ona prolazi;
2) problemi na tangenti koju daje njen nagib.

Obuka u rješavanju tangentnih problema obavljena je korištenjem algoritma koji je predložio A.G. Mordkovich. Njegovo fundamentalna razlika od već poznatih je da je apscisa tačke tangente označena slovom a (umjesto x0), te stoga jednadžba tangente ima oblik

y = f(a) + f "(a)(x – a)

(uporedi sa y = f(x 0) + f "(x 0)(x – x 0)). Ova metodološka tehnika, po našem mišljenju, omogućava studentima da brzo i lako shvate gdje su upisane koordinate trenutne tačke. opšta jednačina tangente i gde su tačke dodira.

Algoritam za sastavljanje tangentne jednadžbe na graf funkcije y = f(x)

1. Označite apscisu tačke tangente slovom a.
2. Naći f(a).
3. Pronađite f "(x) i f "(a).
4. Zamijenite pronađene brojeve a, f(a), f "(a). opšta jednačina tangenta y = f(a) = f "(a)(x – a).

Ovaj algoritam se može sastaviti na osnovu samostalnog identifikacije operacija od strane učenika i redosleda njihove implementacije.

Praksa je pokazala da uzastopno rješavanje svakog od ključnih problema pomoću algoritma omogućava da razvijete vještine pisanja jednadžbe tangente na graf funkcije u fazama, a koraci algoritma služe kao referentne točke za radnje. . Ovaj pristup odgovara teoriji postupnog formiranja mentalnih radnji koju je razvio P.Ya. Galperin i N.F. Talyzina.

U prvoj vrsti zadataka identifikovana su dva ključna zadatka:

tangenta prolazi kroz tačku koja leži na krivulji (problem 1);
tangenta prolazi kroz tačku koja ne leži na krivulji (problem 2).

Zadatak 1. Napišite jednačinu za tangentu na graf funkcije u tački M(3; – 2).

Rješenje. Tačka M(3; – 2) je tačka tangente, pošto

1. a = 3 – apscisa tangentne tačke.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – jednačina tangente.

Zadatak 2. Napišite jednačine svih tangenti na graf funkcije y = – x 2 – 4x + 2 koja prolazi kroz tačku M(– 3; 6).

Rješenje. Tačka M(– 3; 6) nije tangentna tačka, jer je f(– 3) 6 (slika 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – jednačina tangente.

Tangenta prolazi kroz tačku M(– 3; 6), pa njene koordinate zadovoljavaju jednačinu tangente.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = – 4, a 2 = – 2.

Ako je a = – 4, onda je tangentna jednadžba y = 4x + 18.

Ako je a = – 2, onda tangentna jednadžba ima oblik y = 6.

U drugoj vrsti ključni zadaci će biti sljedeći:

tangenta je paralelna nekoj pravoj (problem 3);
tangenta prolazi pod određenim uglom na datu pravu (problem 4).

Zadatak 3. Napišite jednačine svih tangenti na graf funkcije y = x 3 – 3x 2 + 3, paralelno s pravom y = 9x + 1.

1. a – apscisa tačke tangente.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Ali, s druge strane, f"(a) = 9 (uslov paralelizma). To znači da trebamo riješiti jednačinu 3a 2 – 6a = 9. Njeni korijeni su a = – 1, a = 3 (Sl. 3 ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – jednačina tangente;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – jednačina tangente.

Zadatak 4. Napišite jednačinu tangente na graf funkcije y = 0,5x 2 – 3x + 1, koja prolazi pod uglom od 45° na pravu liniju y = 0 (slika 4).

Rješenje. Iz uslova f "(a) = tan 45° nalazimo a: a – 3 = 1 ^ a = 4.

1. a = 4 – apscisa tangentne tačke.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – jednačina tangente.

Lako je pokazati da se rješenje bilo kojeg drugog problema svodi na rješavanje jednog ili više ključnih problema. Razmotrite sljedeća dva problema kao primjer.

1. Napišite jednačine tangenti na parabolu y = 2x 2 – 5x – 2, ako se tangente sijeku pod pravim uglom i jedna od njih dodiruje parabolu u tački sa apscisom 3 (slika 5).

Rješenje. Pošto je data apscisa tačke tangente, prvi dio rješenja svodi se na ključni problem 1.

1. a = 3 – apscisa tangentne tačke jedne od stranica pravi ugao.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – jednačina prve tangente.

Neka je a ugao nagiba prve tangente. Pošto su tangente okomite, onda je ugao nagiba druge tangente. Iz jednačine y = 7x – 20 prve tangente imamo tg a = 7. Nađimo

To znači da je nagib druge tangente jednak .

Dalje rješenje se svodi na ključni zadatak 3.

Neka je B(c; f(c)) tačka dodira druge linije

1. – apscisa druge tačke dodira.
2.
3.
4.
– jednačina druge tangente.

Bilješka. Ugaoni koeficijent tangente može se lakše pronaći ako učenici znaju omjer koeficijenata okomitih pravih k 1 k 2 = – 1.

2. Napišite jednačine svih zajedničkih tangenti na grafove funkcija

Rješenje. Problem se svodi na pronalaženje apscise tačaka dodira zajedničkih tangenti, odnosno na rješavanje ključnog problema 1 u opšti pogled, sastavljanje sistema jednačina i njegovo naknadno rješenje (slika 6).

1. Neka je a apscisa tačke tangente koja leži na grafu funkcije y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Neka je c apscisa tačke tangente koja leži na grafu funkcije
2.
3. f "(c) = c.
4.

Pošto su tangente opšte, onda

Dakle, y = x + 1 i y = – 3x – 3 su zajedničke tangente.

Osnovni cilj razmatranih zadataka je pripremiti učenike da samostalno prepoznaju vrstu ključnog problema pri rješavanju više složeni zadaci, koje zahtijevaju određene istraživačke vještine (sposobnost analize, poređenja, generalizacije, postavljanja hipoteze, itd.). Takvi zadaci uključuju svaki zadatak u kojem je ključni zadatak uključen kao komponenta. Razmotrimo kao primjer problem (inverzan zadatku 1) nalaženja funkcije iz porodice njenih tangenta.

3. Za koje su b i c prave y = x i y = – 2x tangente na grafik funkcije y = x 2 + bx + c?

Neka je t apscisa tačke dodira prave linije y = x sa parabolom y = x 2 + bx + c; p je apscisa tačke dodira prave linije y = – 2x sa parabolom y = x 2 + bx + c. Tada će jednačina tangente y = x poprimiti oblik y = (2t + b)x + c – t 2 , a jednačina tangente y = – 2x će imati oblik y = (2p + b)x + c – p 2 .

Sastavimo i riješimo sistem jednačina

odgovor:

Članak daje detaljno objašnjenje definicija, geometrijsko značenje izvod sa grafičkim oznakama. Jednadžba tangente će se razmatrati na primjerima, naći će se jednadžbe tangente na krivulje 2. reda.

Yandex.RTB R-A-339285-1 Definicija 1

Ugao nagiba prave linije y = k x + b naziva se ugao α, koji se mjeri od pozitivnog smjera ose x do prave linije y = k x + b u pozitivnom smjeru.

Na slici je smjer x označen zelenom strelicom i zelenim lukom, a ugao nagiba crvenim lukom. Plava linija se odnosi na pravu liniju.

Definicija 2

Nagib prave linije y = k x + b naziva se numerički koeficijent k.

Ugaoni koeficijent jednak je tangenti prave, drugim riječima k = t g α.

Ugao nagiba prave linije jednak je 0 samo ako je paralelna oko x, a nagib jednak nuli, jer je tangenta nule jednaka 0. To znači da će oblik jednačine biti y = b.
Ako je ugao nagiba prave linije y = k x + b oštar, tada su ispunjeni uslovi 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, a na grafu se povećava.
Ako je α = π 2, tada je lokacija prave okomita na x. Jednakost je specificirana sa x = c pri čemu je vrijednost c realan broj.
Ako je ugao nagiba prave linije y = k x + b tup, onda odgovara uslovima π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definicija 3

Sekansa je prava koja prolazi kroz 2 tačke funkcije f (x). Drugim riječima, sekansa je prava linija koja se povlači kroz bilo koje dvije tačke na grafu datu funkciju.

Slika pokazuje da je A B sekansa, a f (x) je crna kriva, α je crveni luk, koji označava ugao nagiba sekansa.

Kada je ugaoni koeficijent prave linije jednak tangenti ugla nagiba, jasno je da se tangenta iz pravouglog trokuta A B C može naći iz relacije Suprotna strana na susednu.

Definicija 4

Dobijamo formulu za pronalaženje sekante oblika:

k = t g α = B C A C = f (x B) - f x A x B - x A, gdje su apscise tačaka A i B vrijednosti x A, x B i f (x A), f (x B) su funkcije vrijednosti u ovim tačkama.

Očigledno, kutni koeficijent sekante se određuje pomoću jednakosti k = f (x B) - f (x A) x B - x A ili k = f (x A) - f (x B) x A - x B , a jednačina se mora napisati kao y = f (x B) - f (x A) x B - x A x - x A + f (x A) ili
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekanta vizualno dijeli graf na 3 dijela: lijevo od tačke A, od A do B, desno od B. Slika ispod pokazuje da postoje tri sekante koje se smatraju podudarnim, odnosno postavljene su pomoću slična jednačina.

Po definiciji je jasno da se prava linija i njena sekansa u ovom slučaju poklapaju.

Sekansa može više puta preseći graf date funkcije. Ako postoji jednačina oblika y = 0 za sekantu, tada je broj tačaka preseka sa sinusoidom beskonačan.

Definicija 5

Tangenta na graf funkcije f (x) u tački x 0 ; f (x 0) je prava linija koja prolazi kroz datu tačku x 0; f (x 0), uz prisustvo segmenta koji ima mnogo x vrijednosti blizu x 0.

Primjer 1

Pogledajmo pobliže primjer u nastavku. Tada je jasno da se prava definirana funkcijom y = x + 1 smatra tangentnom na y = 2 x u tački s koordinatama (1; 2). Radi jasnoće, potrebno je razmotriti grafove sa vrijednostima bliskim (1; 2). Funkcija y = 2 x je prikazana crnom bojom, plava linija je tangentna linija, a crvena tačka je tačka preseka.

Očigledno, y = 2 x spaja se s pravom y = x + 1.

Da bismo odredili tangentu, treba razmotriti ponašanje tangente A B dok se tačka B beskonačno približava tački A. Radi jasnoće, predstavljamo crtež.

Sekansa A B, označena plavom linijom, teži položaju same tangente, a ugao nagiba sekansa α počeće da teži uglu nagiba same tangente α x.

Definicija 6

Tangenta na graf funkcije y = f (x) u tački A smatra se graničnim položajem sekante A B dok B teži ka A, odnosno B → A.

Sada idemo dalje na razmatranje geometrijskog značenja derivacije funkcije u tački.

Prijeđimo na razmatranje sekante A B za funkciju f (x), gdje je A i B sa koordinatama x 0, f (x 0) i x 0 + ∆ x, f (x 0 + ∆ x), a ∆ x je označen kao prirast argumenta . Sada će funkcija imati oblik ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Radi jasnoće, dajmo primjer crteža.

Razmotrimo rezultat pravougaonog trougla A B C. Za rješavanje koristimo definiciju tangente, odnosno dobijamo relaciju ∆ y ∆ x = t g α . Iz definicije tangente slijedi da je lim ∆ x → 0 ∆ y ∆ x = t g α x . Prema pravilu derivacije u tački, imamo da se izvod f (x) u tački x 0 naziva granicom omjera prirasta funkcije i priraštaja argumenta, gdje je ∆ x → 0 , onda ga označavamo kao f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Iz toga slijedi da je f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, gdje je k x označen kao nagib tangente.

To jest, nalazimo da f ' (x) može postojati u tački x 0, i kao tangenta na dati graf funkcije u tački tangentnosti jednakoj x 0, f 0 (x 0), gdje je vrijednost nagib tangente u tački jednak je izvodu u tački x 0 . Tada dobijamo da je k x = f " (x 0) .

Geometrijsko značenje derivacije funkcije u tački je da daje koncept postojanja tangente na graf u istoj tački.

Za pisanje jednačine bilo koje prave linije na ravni potrebno je imati ugaoni koeficijent sa tačkom kroz koju ona prolazi. Njegova notacija se uzima kao x 0 na raskrsnici.

Tangentna jednadžba na graf funkcije y = f (x) u tački x 0, f 0 (x 0) ima oblik y = f "(x 0) x - x 0 + f (x 0).

To znači da konačna vrijednost derivacije f"(x 0) može odrediti položaj tangente, odnosno vertikalno, pod uslovom da je lim x → x 0 + 0 f "(x) = ∞ i lim x → x 0 - 0 f "(x ) = ∞ ili odsustvo uopšte pod uslovom lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Položaj tangente zavisi od vrednosti njenog ugaonog koeficijenta k x = f "(x 0). Kada je paralelna sa o x osom, dobijamo da je k k = 0, kada je paralelna sa o y - k x = ∞, a oblik tangentna jednačina x = x 0 raste sa k x > 0, opada kao k x< 0 .

Primjer 2

Sastaviti jednadžbu za tangentu na graf funkcije y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 u tački sa koordinatama (1; 3) i odrediti ugao nagiba.

Rješenje

Po uslovu imamo da je funkcija definirana za sve realne brojeve. Nalazimo da je tačka sa koordinatama određenim uslovom, (1; 3) tačka tangentnosti, tada je x 0 = - 1, f (x 0) = - 3.

Potrebno je pronaći izvod u tački sa vrijednošću - 1. Shvatili smo to

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Vrijednost f' (x) u tački tangente je nagib tangente, koji je jednak tangenti nagiba.

Tada je k x = t g α x = y " (x 0) = 3 3

Iz toga slijedi da je α x = a r c t g 3 3 = π 6

odgovor: tangentna jednačina poprima oblik

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Radi jasnoće dajemo primjer na grafičkoj ilustraciji.

Crna boja se koristi za graf originalne funkcije, Plava boja– slika tangente, crvena tačka – tačka tangente. Slika desno prikazuje uvećani prikaz.

Primjer 3

Odrediti postojanje tangente na graf date funkcije
y = 3 · x - 1 5 + 1 u tački sa koordinatama (1 ; 1) . Napišite jednačinu i odredite ugao nagiba.

Rješenje

Pod uslovom imamo da se domenom definicije date funkcije smatra skup svih realnih brojeva.

Idemo dalje na pronalaženje derivata

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Ako je x 0 = 1, onda je f' (x) nedefinisan, ali su granice zapisane kao lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ i lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , što znači postojanje vertikalne tangente u tački (1; 1).

odgovor: jednadžba će dobiti oblik x = 1, gdje će ugao nagiba biti jednak π 2.

Radi jasnoće, opišimo to grafički.

Primjer 4

Pronađite tačke na grafu funkcije y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, gdje je

Ne postoji tangenta;
Tangenta je paralelna sa x;
Tangenta je paralelna pravoj y = 8 5 x + 4.

Rješenje

Potrebno je obratiti pažnju na obim definicije. Po uslovu imamo da je funkcija definirana na skupu svih realnih brojeva. Proširujemo modul i rješavamo sistem s intervalima x ∈ - ∞ ; 2 i [ - 2 ; + ∞) . Shvatili smo to

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Potrebno je razlikovati funkciju. Imamo to

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Kada je x = − 2, onda izvod ne postoji jer jednostrane granice nisu jednake u toj tački:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Izračunavamo vrijednost funkcije u tački x = - 2, odakle to dobijamo

y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, odnosno tangenta u tački ( - 2; - 2) neće postojati.
Tangenta je paralelna sa x kada je nagib nula. Tada je k x = t g α x = f "(x 0). Odnosno, potrebno je pronaći vrijednosti takvog x kada ga derivacija funkcije okrene na nulu. To jest, vrijednosti f ' (x) će biti tačke tangente, gde je tangenta paralelna sa x.

Kada je x ∈ - ∞ ; - 2, zatim - 1 5 (x 2 + 12 x + 35) = 0, a za x ∈ (- 2; + ∞) dobijamo 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Izračunajte odgovarajuće vrijednosti funkcije

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Dakle - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 se smatraju traženim tačkama grafa funkcije.

Hajde da razmotrimo grafička slika rješenja.

Crna linija je graf funkcije, a crvene tačke su dodirne tačke.

Kada su prave paralelne, ugaoni koeficijenti su jednaki. Zatim je potrebno tražiti tačke na grafu funkcije u kojima će nagib biti jednak vrijednosti 8 5. Da biste to učinili, morate riješiti jednačinu oblika y"(x) = 8 5. Tada, ako je x ∈ - ∞; - 2, dobijamo da je - 1 5 (x 2 + 12 x + 35) = 8 5, a ako je x ∈ ( - 2 ; + ∞), onda je 1 5 (x 2 - 4 x + 3) = 8 5.

Prva jednadžba nema korijen jer je diskriminant manji od nule. Hajde da to zapišemo

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Dakle, druga jednadžba ima dva realna korijena

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Idemo dalje na pronalaženje vrijednosti funkcije. Shvatili smo to

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Bodovi sa vrijednostima - 1; 4 15, 5; 8 3 su tačke u kojima su tangente paralelne pravoj y = 8 5 x + 4.

odgovor: crna linija – grafik funkcije, crvena linija – grafik od y = 8 5 x + 4, plava linija – tangente u tačkama - 1; 4 15, 5; 8 3.

Može postojati beskonačan broj tangenata za date funkcije.

Primjer 5

Napišite jednadžbe svih raspoloživih tangenta funkcije y = 3 cos 3 2 x - π 4 - 1 3, koje se nalaze okomito na pravu liniju y = - 2 x + 1 2.

Rješenje

Za sastavljanje jednačine tangente potrebno je pronaći koeficijent i koordinate tačke tangente, na osnovu uslova okomitosti pravih. Definicija je sljedeća: proizvod ugaonih koeficijenata koji su okomiti na prave je jednak - 1, odnosno zapisan kao k x · k ⊥ = - 1. Iz uslova imamo da je ugaoni koeficijent lociran okomito na pravu i jednak je k ⊥ = - 2, tada je k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Sada morate pronaći koordinate dodirnih tačaka. Morate pronaći x, a zatim njegovu vrijednost za datu funkciju. Imajte na umu da iz geometrijskog značenja derivacije u tački
x 0 dobijamo da je k x = y "(x 0). Iz ove jednakosti nalazimo vrijednosti x za tačke dodira.

Shvatili smo to

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Ovo trigonometrijska jednačinaće se koristiti za izračunavanje ordinata tangentnih tačaka.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk ili 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk ili 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk ili x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z je skup cijelih brojeva.

x je pronađeno kontaktnih tačaka. Sada morate prijeći na traženje vrijednosti y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 ili y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 ili y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 ili y 0 = - 4 5 + 1 3

Iz ovoga dobijamo da je 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 su tačke dodira.

odgovor: potrebne jednačine će biti zapisane kao

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Za vizualni prikaz, razmotrite funkciju i tangentu na koordinatnoj liniji.

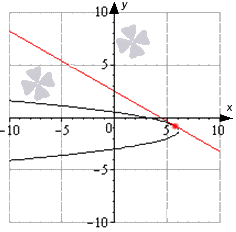
Slika pokazuje da se funkcija nalazi na intervalu [ - 10 ; 10 ], gdje je crna linija grafik funkcije, plave linije su tangente, koje se nalaze okomito na datu liniju oblika y = - 2 x + 1 2. Crvene tačke su dodirne tačke.

Kanonske jednadžbe krivulja 2. reda nisu jednovrijedne funkcije. Tangentne jednadžbe za njih se sastavljaju prema poznatim shemama.

Tangenta na kružnicu

Definirati kružnicu sa centrom u tački x c e n t e r ; y c e n t e r i radijus R, primijenimo formulu x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Ova jednakost se može napisati kao unija dvije funkcije:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Prva funkcija se nalazi na vrhu, a druga na dnu, kao što je prikazano na slici.

Sastaviti jednadžbu kružnice u tački x 0; y 0 , koji se nalazi u gornjem ili donjem polukrugu, trebali biste pronaći jednadžbu grafika funkcije oblika y = R 2 - x - x c e n t e r 2 + y c e n t e r ili y = - R 2 - x - x c e n t + e y c e n t e r na naznačenoj tački.

Kada je u tačkama x c e n t e r ; y c e n t e r + R i x c e n t e r ; y c e n t e r - R tangente se mogu dati jednadžbama y = y c e n t e r + R i y = y c e n t e r - R , a u tačkama x c e n t e r + R ; y c e n t e r i
x c e n t e r - R ; y c e n t e r će biti paralelan sa o y, tada ćemo dobiti jednačine oblika x = x c e n t e r + R i x = x c e n t e r - R .

Tangenta na elipsu

Kada elipsa ima centar u x c e n t e r ; y c e n t e r sa poluosama a i b, onda se može odrediti pomoću jednačine x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Elipsa i krug se mogu označiti kombinacijom dvije funkcije, odnosno gornje i donje poluelipse. Onda to shvatamo

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Ako se tangente nalaze na vrhovima elipse, onda su paralelne oko x ili oko y. U nastavku, radi jasnoće, razmotrite sliku.

Primjer 6

Napišite jednadžbu tangente na elipsu x - 3 2 4 + y - 5 2 25 = 1 u tačkama sa vrijednostima x jednakim x = 2.

Rješenje

Potrebno je pronaći tangente koje odgovaraju vrijednosti x = 2. Zamjenjujemo postojeću jednačinu elipse i nalazimo je

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Tada je 2 ; 5 3 2 + 5 i 2; - 5 3 2 + 5 su tangente koje pripadaju gornjoj i donjoj poluelipsi.

Pređimo na pronalaženje i rješavanje jednadžbe elipse u odnosu na y. Shvatili smo to

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Očigledno, gornja poluelipsa je specificirana pomoću funkcije oblika y = 5 + 5 2 4 - x - 3 2, a donja poluelipsa y = 5 - 5 2 4 - x - 3 2.

Primijenimo standardni algoritam za kreiranje jednadžbe za tangentu na graf funkcije u tački. Zapišimo da je jednačina za prvu tangentu u tački 2; 5 3 2 + 5 će izgledati

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Nalazimo da je jednačina druge tangente sa vrijednošću u tački
2 ; - 5 3 2 + 5 poprima oblik

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafički, tangente su označene na sljedeći način:

Tangenta na hiperbolu

Kada hiperbola ima centar u x c e n t e r ; y c e n t e r i vrhovi x c e n t e r + α ; y c e n t e r i x c e n t e r - α ; y c e n t e r , postoji nejednakost x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, ako je sa vrhovima x c e n t e r ; y c e n t e r + b i x c e n t e r ; y c e n t e r - b , tada se specificira pomoću nejednakosti x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbola se može predstaviti kao dvije kombinovane funkcije oblika

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r ili y = b a · (x - x n + c2) e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

U prvom slučaju imamo da su tangente paralelne sa y, au drugom paralelne sa x.

Iz toga slijedi da je za pronalaženje jednačine tangente na hiperbolu potrebno saznati kojoj funkciji pripada tačka tangente. Da bi se to utvrdilo, potrebno je izvršiti zamjenu u jednadžbe i provjeriti identitet.

Primjer 7

Napišite jednačinu za tangentu na hiperbolu x - 3 2 4 - y + 3 2 9 = 1 u tački 7; - 3 3 - 3 .

Rješenje

Za pronalaženje hiperbole potrebno je transformirati zapis rješenja pomoću 2 funkcije. Shvatili smo to

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 i y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Potrebno je identifikovati kojoj funkciji pripada data tačka sa koordinatama 7; - 3 3 - 3 .

Očigledno, za provjeru prve funkcije potrebno je y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, tada tačka ne pripada grafu, pošto jednakost ne važi.

Za drugu funkciju imamo da je y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, što znači da tačka pripada datom grafu. Odavde biste trebali pronaći padinu.

Shvatili smo to

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

odgovor: tangentna jednačina se može predstaviti kao

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Jasno je prikazano ovako:

Tangenta na parabolu

Da biste kreirali jednadžbu za tangentu na parabolu y = a x 2 + b x + c u tački x 0, y (x 0), morate koristiti standardni algoritam, tada će jednadžba imati oblik y = y "(x 0) x - x 0 + y ( x 0). Takva tangenta na vrhu je paralelna sa x.

Trebali biste definirati parabolu x = a y 2 + b y + c kao uniju dvije funkcije. Stoga moramo riješiti jednačinu za y. Shvatili smo to

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Grafički prikazano kao:

Da biste saznali da li tačka x 0, y (x 0) pripada funkciji, postupajte lagano prema standardnom algoritmu. Takva tangenta će biti paralelna sa o y u odnosu na parabolu.

Primjer 8

Napišite jednačinu tangente na graf x - 2 y 2 - 5 y + 3 kada imamo ugao tangente od 150°.

Rješenje

Rješenje započinjemo predstavljanjem parabole kao dvije funkcije. Shvatili smo to

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Vrijednost nagiba jednaka je vrijednosti derivacije u tački x 0 ove funkcije i jednaka je tangentu ugla nagiba.

Dobijamo:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

Odavde određujemo x vrijednost za tačke kontakta.

Prva funkcija će biti napisana kao

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Očigledno, nema pravih korijena, jer smo dobili negativnu vrijednost. Zaključujemo da za takvu funkciju ne postoji tangenta sa uglom od 150°.

Druga funkcija će biti napisana kao

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Imamo da su dodirne tačke 23 4 ; - 5 + 3 4 .

odgovor: tangentna jednačina poprima oblik

y = - 1 3 x - 23 4 + - 5 + 3 4

Prikažimo to grafički na ovaj način:

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

U ovom članku ćemo analizirati sve vrste problema koje treba pronaći

Podsjetimo se geometrijsko značenje derivacije: ako je tangenta nacrtana na graf funkcije u tački, tada je koeficijent nagiba tangente (jednak tangentu ugla između tangente i pozitivnog smjera osa) jednaka je derivaciji funkcije u tački.

Uzmimo proizvoljnu tačku na tangenti sa koordinatama:

I razmislite o pravokutnom trokutu:

U ovom trouglu

Odavde

Ovo je jednadžba tangente povučene na graf funkcije u tački.

Da bismo napisali jednadžbu tangente, potrebno je samo znati jednadžbu funkcije i tačku u kojoj je tangenta nacrtana. Tada možemo pronaći i .

Postoje tri glavna tipa problema tangentnih jednačina.

1. Date kontaktnu tačku

2. Dat je koeficijent nagiba tangente, odnosno vrijednost derivacije funkcije u tački.

3. Date su koordinate tačke kroz koju je povučena tangenta, ali koja nije tačka tangente.

Pogledajmo svaku vrstu zadatka.

1 . Napišite jednadžbu tangente na graf funkcije u tački .

b) Pronađite vrijednost derivacije u tački . Prvo pronađimo derivaciju funkcije

Zamijenimo pronađene vrijednosti u tangentnu jednadžbu:

Otvorimo zagrade na desnoj strani jednačine. Dobijamo:

odgovor: .

2. Pronađite apscisu tačaka u kojima su funkcije tangente na graf paralelno sa x-osom.

Ako je tangenta paralelna sa x-osi, stoga je ugao između tangente i pozitivnog smjera ose nula, stoga je tangenta kuta tangente nula. To znači da je vrijednost derivacije funkcije na dodirnim tačkama je nula.

a) Naći derivaciju funkcije .

b) Izjednačimo derivaciju sa nulom i pronađemo vrijednosti u kojima je tangenta paralelna s osom:

Izjednačavajući svaki faktor sa nulom, dobijamo:

Odgovor: 0;3;5

3. Napišite jednadžbe za tangente na graf funkcije , paralelno ravno .

Tangenta je paralelna pravoj. Nagib ove linije je -1. Pošto je tangenta paralelna sa ovom pravom, nagib tangente je takođe -1. To je znamo nagib tangente, i, samim tim, vrijednost derivata u tački tangente.

Ovo je druga vrsta problema za pronalaženje tangentne jednačine.

Dakle, data nam je funkcija i vrijednost derivacije u tački tangente.

a) Pronađite tačke u kojima je derivacija funkcije jednaka -1.

Prvo, pronađimo jednačinu derivata.

Izjednačimo derivaciju sa brojem -1.

Nađimo vrijednost funkcije u tački.

(po stanju)

b) Nađimo jednačinu tangenta na graf funkcije u tački .

Nađimo vrijednost funkcije u tački.

(po stanju).

Zamijenimo ove vrijednosti u tangentnu jednadžbu:

odgovor:

4 . Napišite jednadžbu tangente na krivu , prolazeći kroz tačku

Prvo, hajde da proverimo da li je tačka tačka tangente. Ako je tačka tangentna tačka, tada pripada grafu funkcije, a njene koordinate moraju zadovoljiti jednadžbu funkcije. Zamenimo koordinate tačke u jednadžbu funkcije.

Title="1sqrt(8-3^2)">. Мы получили под корнем !} negativan broj, jednakost nije tačna, a tačka ne pripada grafu funkcije i nije kontaktna tačka.

Ovo je posljednja vrsta problema za pronalaženje tangentne jednačine. Prva stvar moramo pronaći apscisu tačke tangente.

Hajde da nađemo vrednost.

Neka bude tačka kontakta. Tačka pripada tangenti na graf funkcije. Ako zamenimo koordinate ove tačke u tangentnu jednačinu, dobićemo tačnu jednakost:

Vrijednost funkcije u tački je .

Nađimo vrijednost derivacije funkcije u tački.

Prvo, pronađimo derivaciju funkcije. Ovo .

Izvod u tački je jednak .

Zamijenimo izraze za i u tangentnu jednadžbu. Dobijamo jednačinu za:

Hajde da riješimo ovu jednačinu.

Smanjite brojilac i imenilac razlomka za 2:

Hajde da damo desna strana jednadžbe na zajednički nazivnik. Dobijamo:

Pojednostavimo brojilac razlomka i pomnožimo obje strane sa - ovaj izraz je striktno veći od nule.

Dobijamo jednačinu

Hajde da to rešimo. Da bismo to učinili, kvadriramo oba dijela i prijeđimo na sistem.

Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0) ) ))( )">!}

Rešimo prvu jednačinu.

Hajde da odlučimo kvadratna jednačina, dobijamo

Drugi korijen ne zadovoljava uslov title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}

Napišimo jednačinu tangente na krivu u tački. Da biste to učinili, zamijenite vrijednost u jednadžbu - Već smo to snimili.

odgovor:
.

Ovaj matematički program pronalazi jednadžbu tangente na graf funkcije $f(x)$ u korisnički specificiranoj tački $a$.

Program ne samo da prikazuje tangentnu jednačinu, već prikazuje i proces rješavanja problema.

Ovaj online kalkulator može biti koristan srednjoškolcima u pripremi za testovi i ispiti, prilikom provjere znanja prije Jedinstvenog državnog ispita, za roditelje za kontrolu rješavanja mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo unajmiti nastavnika ili kupiti nove udžbenike? Ili samo želite da to završite što je brže moguće? zadaća iz matematike ili algebre? U tom slučaju možete koristiti i naše programe sa detaljnim rješenjima.

Na taj način možete sami provoditi obuku i/ili obuku vaše mlađe braće ili sestara, dok se nivo obrazovanja u oblasti rješavanja problema povećava.

Ako trebate pronaći izvod funkcije, onda za to imamo zadatak Pronađite izvod.

Ako niste upoznati s pravilima za unos funkcija, preporučujemo da se upoznate s njima.

Unesite izraz funkcije $f(x)$ i broj $a$ Pronađite jednadžbu tangente

Otkriveno je da neke skripte potrebne za rješavanje ovog problema nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

JavaScript je onemogućen u vašem pretraživaču.
Da bi se rješenje pojavilo, morate omogućiti JavaScript.
Evo instrukcija kako da omogućite JavaScript u vašem pretraživaču.

Jer Ima puno ljudi koji su voljni da riješe problem, vaš zahtjev je stavljen u red čekanja.
Za nekoliko sekundi rješenje će se pojaviti ispod.
Pričekajte sec...

Ako ti uočio grešku u rješenju, onda o tome možete pisati u Obrascu za povratne informacije.
Nemoj zaboraviti naznačiti koji zadatak ti odluči šta unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Direktan nagib

Podsjetimo da je raspored linearna funkcija$y=kx+b$ je prava linija. Poziva se broj $k=tg \alpha $. nagib prave linije, a ugao $\alpha $ je ugao između ove linije i Ox ose

Ako je $k>0$, onda \(0 If \(kJednačina tangente na graf funkcije

Ako tačka M(a; f(a)) pripada grafu funkcije y = f(x) i ako se u ovoj tački može povući tangenta na graf funkcije koja nije okomita na x-osu, onda iz geometrijskog značenja derivacije slijedi da je kutni koeficijent tangente jednak f"(a). Zatim ćemo razviti algoritam za sastavljanje jednadžbe za tangentu na graf bilo koje funkcije.

Neka su funkcija y = f(x) i tačka M(a; f(a)) date na grafu ove funkcije; neka bude poznato da f"(a) postoji. Napravimo jednačinu za tangentu na graf date funkcije u dati poen. Ova jednadžba, kao i jednadžba bilo koje prave linije koja nije paralelna s ordinatnom osom, ima oblik y = kx + b, pa je zadatak pronaći vrijednosti koeficijenata k i b.

Sve je jasno sa ugaonim koeficijentom k: poznato je da je k = f"(a). Za izračunavanje vrijednosti b koristimo činjenicu da željena prava linija prolazi kroz tačku M(a; f(a)) To znači da ako zamenimo koordinate tačke M u jednačinu prave, dobijamo tačnu jednakost: $f(a)=ka+b$, tj. $b = f(a) - ka$.

Ostaje zamijeniti pronađene vrijednosti koeficijenata k i b u jednadžbu prave linije:

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a )(x-a) $$

Primili smo jednadžba tangente na graf funkcije$y = f(x) $ u tački $x=a $.

Algoritam za pronalaženje jednačine tangente na graf funkcije $y=f(x)$
1. Označite apscisu tačke tangente slovom $a$
2. Izračunajte $f(a)$
3. Pronađite $f"(x)$ i izračunajte $f"(a)$
4. Zamijenite pronađene brojeve $a, f(a), f"(a) $ u formulu $y=f(a)+ f"(a)(x-a) $

Knjige (udžbenici) Sažeci Jedinstvenog državnog ispita i Jedinstvenog državnog ispita online Igre, zagonetke Iscrtavanje grafova funkcija Pravopisni rječnik ruskog jezika Rječnik omladinskog slenga Katalog ruskih škola Katalog srednjih obrazovnih institucija Rusije Katalog ruskih univerziteta Lista problema Pronalaženje GCD i LCM Pojednostavljivanje polinoma (množenje polinoma)

f(x)=
a=

Br formula jednadžbe tangente. Online kalkulator

Tangenta na kružnicu

Tangenta na elipsu

Tangenta na hiperbolu

Tangenta na parabolu

Malo teorije.

Direktan nagib