Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:

F " (x) = f(x). (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

Если F(x) - какая-нибудь первобразная для функции f(x), то ∫ f(x)dx = F(x) + C, (8.2)

где С- произвольная постоянная.

Таблица интегралов

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Список табличных интегралов

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = arctg x + C

8. = arcsin x + C

10. = - ctg x + C

Замена переменной

Для интегрирования многих функций применяют метод замены переменной или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [α,β], функция z =g(x) имеет на непрерывную производную и α ≤ g(x) ≤ β, то

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Например:

Метод интегрирования по частям

Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные . Тогда, по произведения,

d(uv))= udv + vdu или udv = d(uv) - vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv - ∫ vdu (8.4.)

Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv"dx к интегрированию выражения vdu=vu"dx.

Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.

Определенный интеграл

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [ a,b] на n частей точками a= x 0 < x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1 . Сумма вида f(ξ i)Δ x i называется интегральной суммой , а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

F(ξ i)Δx i (8.5).

Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .

Для определенного интеграла справедливы следующие свойства:

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Последнее свойство называется теоремой о среднем значении .

Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл

∫f(x)dx = F(x) + C

и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:

F(b) - F(a). (8.6)

Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox .

Несобственные интегралы

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:

(8.7)

Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится .

Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

если эти пределы существуют и конечны. Обозначение:

Примеры вычисления интегралов

Пример 3.30. Вычислить ∫dx/(x+2).

Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .

Пример 3.31 . Найти ∫ tgxdx.

Решение. ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Пример 3.32 . Найти ∫dx/sinx

Решение.

Пример 3.33. Найти .

Решение. = .

Пример 3.34 . Найти ∫arctgxdx.

Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример 3.35 . Вычислить ∫lnxdx.

Решение. Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Пример 3.36 . Вычислить ∫e x sinxdx.

Решение. Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интеграл ∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx, du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получили соотношение ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, откуда 2∫e x sinx dx = - e x cosx + e x sinx + С.

Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.

Решение. Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Вычислить J = .

Решение. Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = .

Пример 3.39 . Вычислить интеграл J = .

Решение. Имеем: . Поэтому =
=
=. вводится так sqrt(tan(x/2)).

А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.

Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:

Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u , а остальная часть относится ко второму множителю и обозначается через dv . Затем дифференцированием находится du и интегрированием - функция v . При этом за u dv - такую часть подынтегрального выражения, которая легко интегрируется.

Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит :

1) - логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u ;

2) , , - синус, косинус и экспоненту, умноженные на P (x ) - произвольный многочлен от икса, тогда эти функции обозначают через dv , а многочлен - через u ;

3) , , , , в этом случае интегрирование по частям применяется дважды.

Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале урока формулу интегрирования по частям

получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.

Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:

то её можно записать в виде

который и был приведён в самом начале урока.

При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С , равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.

Есть у метода интегрирования по частям совершенно особенное применение: с его помощью можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например, функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула - это формула для нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается последовательным понижением степени. Так, если подынтегральная функция - синус в четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей степени и так далее. Описанной задаче посвящен последний параграф этого урока.

Применяем интегрирование по частям вместе

Пример 1. Найти неопределённый интеграл методом интегрирования по частям :

Решение. В подынтегральном выражении - логарифм, который, как мы уже знаем, разумно обозначить через u . Полагаем, что , .

Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма):

И снова логарифм...

Пример 2. Найти неопределённый интеграл:

Решение. Пусть , .

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
,
.

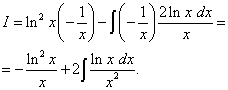
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма).

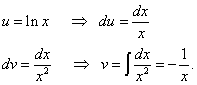
Находим изначальный интеграл:

Пример 3.

Решение. Арктангенс, как и логарифм, лучше обозначить через u . Итак, пусть , .

Тогда ,
.

Применяя формулу интегрирования по частям, получаем:

Второй интеграл находим методом замены переменной.

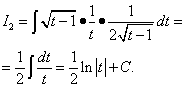
Возвращаясь к переменной x , получаем

.

Находим изначальный интеграл:

.

Пример 4. Найти неопределённый интеграл методом интегрирования по частям :

Решение. Экспоненту лучше обозначить через dv . Разбиваем подынтегральное выражение на два множителя. Полагая, что

Пример 5. Найти неопределённый интеграл методом интегрирования по частям :

.

Решение. Пусть , . Тогда , .

Используя формулу интегрирования по частям (1), находим:

Пример 6. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Синус, как и экспоненту, удобно обозначить через dv . Пусть , .

По формуле интегрирования по частям находим:

Снова применяем интегрирование по частям вместе

Пример 10. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv . Обозначаем , .

Тогда , .

По формуле интегрирования по частям получаем:

Ко второму слагаемому также применяем интегрирование по частям. Обозначаем , .

Применив эти обозначения, интегрируем упомянутое слагаемое:

Теперь находим требуемый интеграл:

Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие, которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из практики известно, что лучше обозначать через u , а что через dv . Поэтому в этих случаях нужно пользоваться соображением удобства, также приведённым в параграфе "Суть метода интегрирования по частям": за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется. Последний пример этого урока - решение именно такого интеграла.

Примеры интегрирования по частям подобного состава задают студентам 1, 2 курсов. Данные задания задавали на контрольной работе в ЛНУ им. И. Франка. Чтобы формулы в задачах и ответах не повторялись же задачи описывать не будем. По условию заданий нужно или "Найти интеграл", или "Вычислить интеграл".
Пример 8. Интеграл находим по правилу интегрирования частями int(u*dv)=u*v-int(v*du). Здесь главное правильно выбрать функции под правило. (Для себя запомните что за dv если возможно выбирают периодические функции или такие, которые при дифференцировании с точностью до множителя дают сами себя - экспонента). В этом интеграле нужно синус внести под дифференциал

Дальнейшее интегрирование достаточно простое и на деталях останавливаться не будем.

Пример 9. Снова нужно применять правило интегрирования по частям u*dv . Здесь имеем произведение периодической функции на экспоненту, поэтому что лучше вносить под дифференциал выбирать Вам. Можно как экспоненту, так и косинус (в каждом варианте получим рекуррентную формулу).

Применяем интегрирование по частям повторно

Пришли к рекуррентной формуле. Если записать интеграл который искали и результат вычислений то получим два подобные слагаемые

Группируем их и находим искомый интеграл


Пример 10. Имеем готовую запись интеграла под правило u*dv. Находим du и выполняем интегрирование


Сводим второй интеграл под табличную формулу и вычисляем его

Пример 11. Обозначим за новую переменную cos(ln(x))=u і найдем du , затем внесением под дифференциал


К интегралу повторно применяем правило интегрирования по частям


Пришли к рекуррентной формуле

с которой и вычисляем неизвестный интеграл

Пример 12. Для нахождения интеграла выделим в знаменателе полный квадрат. Далее сведя знаменатель к известной формуле интегрирования получим арктангенс


Хорошо запомните порядок чередования множителей. Единица разделена на корень из свободного члена фигурирует перед арктангенсом, также этот множитель присутствует в арктангенс перед переменной.
Пример 13. Дело имеем с подобным интегралом, только в знаменателе квадратичная зависимость находится под корнем. Выделяем полный квадрат и сводим под формулу интегрирования, которая дает логарифм


Вот такие бывают примеры на контрольной или тестах. Хорошо запомните основные схемы интегрирования.
Если не можете решить интеграл сами, тогда обращайтесь за помощью.

Определенный интеграл. Примеры решений

И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений . Кроме того, есть pdf-курсы для сверхбыстрой подготовки – если у вас в запасе буквально день, пол дня.

В общем виде определенный интеграл записывается так:

Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования .

Нижний предел интегрирования
Верхний предел интегрирования стандартно обозначается буквой .
Отрезок называется отрезком интегрирования .

Прежде чем мы перейдем к практическим примерам, небольшое faq по определенному интегралу.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница :

Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле не добавляется . Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .

3) Подставляем значение нижнего предела в первообразную функцию: .

4) Рассчитываем (без ошибок!) разность , то есть, находим число.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.

Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования .

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования . По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:

???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл , коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.

– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла .

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак :

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:

– в таком виде интегрировать значительно удобнее.

– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования , правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям :

Пример 1

Решение:

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

. Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2

Вычислить определенный интеграл

Это пример для самостоятельно решения, решение и ответ в конце урока.

Немного усложняем задачу:

Пример 3

Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:

Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.

Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.

Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?

Так, применительно к рассматриваемому примеру: перед тем, как в первообразную функцию подставлять верхний и нижний пределы, желательно на черновике проверить, а правильно ли вообще найден неопределенный интеграл? Дифференцируем:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.

Такая проверка будет не лишней при вычислении любого определенного интеграла .

Пример 4

Вычислить определенный интеграл

Это пример для самостоятельно решения. Попробуйте решить его коротким и подробным способом.

Замена переменной в определенном интеграле

Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле .

В этом параграфе нет ничего страшного или сложного. Новизна состоит в вопросе, как поменять пределы интегрирования при замене .

В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.

Пример 5

Вычислить определенный интеграл

Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: . Но есть одна неувязочка, в табличном интеграле под корнем , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

Сначала готовим наш интеграл к замене:

Из вышеуказанных соображений совершенно естественно напрашивается замена:
Таким образом, в знаменателе будет всё хорошо: .
Выясняем, во что превратится оставшаяся часть подынтегрального выражения, для этого находим дифференциал :

По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.

Находим новые пределы интегрирования .

Это достаточно просто. Смотрим на нашу замену и старые пределы интегрирования , .

Сначала подставляем в выражение замены нижний предел интегрирования, то есть, ноль:

Потом подставляем в выражение замены верхний предел интегрирования, то есть, корень из трёх:

Готово. И всего-то лишь…

Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования .

(2) Это простейший табличный интеграл, интегрируем по таблице. Константу лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования – это подготовка для применения формулы Ньютона-Лейбница.

(3) Используем формулу Ньютона-Лейбница .

Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.

Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо .

А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.

Пример 6

Вычислить определенный интеграл

Пример 7

Вычислить определенный интеграл

Это примеры для самостоятельного решения. Решения и ответы в конце урока.

И в заключение параграфа пара важных моментов, разбор которых появился благодаря посетителям сайта. Первый из них касается правомерности замены . В некоторых случаях её проводить нельзя! Так, Пример 6, казалось бы, разрешим с помощью универсальной тригонометрической подстановки , однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» должна быть непрерывна во всех точках отрезка интегрирования .

В другом электронном письме поступил следующий вопрос: «А нужно ли менять пределы интегрирования, когда мы подводим функцию под знак дифференциала?». Сначала я хотел «отмахнуться от ерунды» и автоматически ответить «конечно, нет», но затем задумался о причине появления такого вопроса и вдруг обнаружил, что информации-то не хватает. А ведь она, пусть и очевидна, но очень важнА:

Если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно ! Почему? Потому что в этом случае нет фактического перехода к новой переменной . Например:

И здесь подведение гораздо удобнее академичной замены с последующей «росписью» новых пределов интегрирования. Таким образом, если определённый интеграл не очень сложен, то всегда старайтесь подвести функцию под знак дифференциала ! Это быстрее, это компактнее, и это обыденно – в чём вы убедитесь ещё десятки раз!

Большое спасибо за ваши письма!

Метод интегрирования по частям в определенном интеграле

Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:

Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения и, после того, как мы возьмем интеграл .

Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.

Пример 8

Вычислить определенный интеграл

Решаем.

Интегрируем по частям:

У кого возникли трудности с интегралом , загляните на урок Интегралы от тригонометрических функций , там он подробно разобран.

(1) Записываем решение в соответствии с формулой интегрирования по частям.

(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!

(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.

Если честно, я недолюбливаю формулу и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.

Вычислить определенный интеграл

На первом этапе я нахожу неопределенный интеграл :

Интегрируем по частям:

Первообразная функция найдена. Константу в данном случае добавлять не имеет смысла.

В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования

На втором этапе я провожу проверку (обычно на черновике).

Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:

Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.

Третий этап – применение формулы Ньютона-Лейбница :

И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле (первым способом), то стопудово где-нибудь допустит ошибку.

Рассмотренный алгоритм решения можно применить для любого определенного интеграла .

Уважаемый студент, распечатай и сохрани:

Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?

1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов .

2) Проверяем найденную первообразную функцию дифференцированием . Если она найдена неверно, третий шаг будет напрасной тратой времени.

3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.

И, на закуску, интеграл для самостоятельного решения.

Пример 9

Вычислить определенный интеграл

Решение и ответ где-то рядом.

Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла?
Интегрируем по частям:

Вы точно их прорешали и получили такие ответы? ;-) И на старуху бывает порнуха.

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача - задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти закон движения.
Решение. Пусть s = s(t) - искомый закон движения. Известно, что s"(t) = v(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна gt. Нетрудно догадаться, что \(s(t) = \frac{gt^2}{2} \). В самом деле
\(s"(t) = \left(\frac{gt^2}{2} \right)" = \frac{g}{2}(t^2)" = \frac{g}{2} \cdot 2t = gt \)
Ответ: \(s(t) = \frac{gt^2}{2} \)

Сразу заметим, что пример решен верно, но неполно. Мы получили \(s(t) = \frac{gt^2}{2} \). На самом деле задача имеет бесконечно много решений: любая функция вида \(s(t) = \frac{gt^2}{2} + C \), где C - произвольная константа, может служить законом движения, поскольку \(\left(\frac{gt^2}{2} +C \right)" = gt \)

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s 0 , то из равенства s(t) = (gt 2)/2 + C получаем: s(0) = 0 + С, т. е. C = s 0 . Теперь закон движения определен однозначно: s(t) = (gt 2)/2 + s 0 .

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например: возведение в квадрат (х 2) и извлечение квадратного корня (\(\sqrt{x} \)), синус (sin x) и арксинус (arcsin x) и т. д. Процесс нахождения производной по заданной функции называют дифференцированием , а обратную операцию, т. е. процесс нахождения функции по заданной производной, - интегрированием .

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у" = f"(x). Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у" = f"(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для \(x \in X \) выполняется равенство F"(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х 2 является первообразной для функции у = 2х, поскольку для любого х справедливо равенство (x 2)" = 2х
2) Функция у = х 3 является первообразной для функции у = 3х 2 , поскольку для любого х справедливо равенство (x 3)" = 3х 2
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство (sin(x))" = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) - первообразная для f(x), то kF(x) - первообразная для kf(x).

Теорема 1. Если y = F(x) - первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция \(y=\frac{1}{k}F(kx+m) \)

Теорема 2. Если y = F(x) - первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл \(\textstyle \int F(x)dx \). Сделаем подстановку \(x= \varphi(t) \) где \(\varphi(t) \) - функция, имеющая непрерывную производную.
Тогда \(dx = \varphi " (t) \cdot dt \) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)

Интегрирование выражений вида \(\textstyle \int \sin^n x \cos^m x dx \)

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям - применение следующей формулы для интегрирования:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
или:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)

Таблица неопределённых интегралов (первообразных) некоторых функций

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac{x^{n+1}}{n+1} +C \;\; (n \neq -1) $$ $$ \int \frac{1}{x} dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac{a^x}{\ln a} +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $$ \int \frac{dx}{\cos^2 x} = \text{tg} x +C $$ $$ \int \frac{dx}{\sin^2 x} = -\text{ctg} x +C $$ $$ \int \frac{dx}{\sqrt{1-x^2}} = \text{arcsin} x +C $$ $$ \int \frac{dx}{1+x^2} = \text{arctg} x +C $$ $$ \int \text{ch} x dx = \text{sh} x +C $$ $$ \int \text{sh} x dx = \text{ch} x +C $$

← Вернуться